2024-12-06

ベイズ統計とは？その仕組みやメリット、活用事例をわかりやすく解説

この記事のポイント

ベイズ統計は、事前の知識を活かして新しい情報で確率を更新できる統計手法
事前確率を基に、新しいデータによって事後確率を更新し、より精度の高い推定が可能
少ないデータでも有効な推論が可能で、医療診断やAIなど幅広い分野で活用されている
確率の更新が可能なため、新しいデータが得られるたびに精度を向上できる
複雑な計算が必要になる場合があるものの、Pythonなどのツールで実装可能

監修者プロフィール

坂本将磨

Microsoft AIパートナー、LinkX Japan代表。東京工業大学大学院で技術経営修士取得、研究領域：自然言語処理、金融工学。NHK放送技術研究所でAI、ブロックチェーン研究に従事。学会発表、国際ジャーナル投稿、経営情報学会全国研究発表大会にて優秀賞受賞。シンガポールでのIT、Web3事業の創業と経営を経て、LinkX Japan株式会社を創業。

統計学の世界では、データに基づいた確実な判断を下すために、さまざまな手法があります。
その中でも特に柔軟なアプローチが求められる場面において、注目されるのがベイズ統計学です。

ベイズ統計学は、事前に持っている信念や情報を数学的手法によって更新し、より精緻な予測や意思決定を可能にします。

この記事では、ベイズ統計の基本原理から具体的な活用例まで、幅広い知見を提供します。
ベイズの定理とは何か、そしてそれが統計学における他のアプローチとどう異なるのかを解説し、実生活や産業界での応用事例を通じて、ベイズ統計の理解を深めます。

データ解析を行ううえでの新たな視点を得たい方は、ぜひ本記事をお読みください。

ベイズ統計とは？

ベイズ統計は、一言で言えば「新しい情報を取り入れて、確率（ものごとの起こりやすさ）を更新する方法」です。

たとえば、友達がよく遅れる人だと知っています（これが事前情報）。でも、今日「友達が予定どおり来るかもしれない」と思う理由ができました（たとえば「今日は特別に早く出たと連絡があった」）。
この新しい情報を取り入れて、「遅れる確率」を少し減らし、「時間どおり来る確率」を高めますよね。これがベイズ統計の基本の考え方です！

ではほかの統計学とは何がちがうのでしょうか？

統計学とは？

統計学は、データを収集、分析、解釈し、そこから有意な結論を導き出す学問分野です。統計学は、記述統計学、推計統計学、ベイズ統計学の大きく3つに分けられます。また、記述統計学、推計統計学をまとめて、頻度統計学ともいいます。

記述統計学

記述統計学イメージ

記述統計学は、データの要約や整理を目的とした手法です。平均、中央値、分散、標準偏差などの統計指標を使って、データの特徴をわかりやすく説明します。具体的には、グラフや数値でデータの傾向を示すことが多いです。

推計統計学

推計統計学イメージ
推計統計学は、サンプルデータから母集団についての推定や予測を行います。例えば、標本を使って母集団の平均を推定したり、仮説検定を用いて仮説が正しいかどうかを確認します。

ベイズ統計学

ベイズ統計学イメージ

ベイズ統計学は、事前確率を基に、新しいデータによって確率を更新する方法です。ベイズの定理に基づき、データが新たに得られるたびに確率を修正し、より精度の高い推定を行います。

ベイズ統計と頻度統計の違い

前章で、3つの統計学について簡単に解説しましたが、ベイズ統計と頻度統計(記述統計、推計統計)にはどのような違いがあるのでしょうか。
ベイズ統計は「柔軟で現実的」、頻度統計は「シンプルで客観的」と考えるとわかりやすいです！
どういうことなのか見ていきましょう

確率の解釈

ベイズ統計の確率は、ある事象に対する主観的な信念の度合いを表します。これは、事前の知識や情報に基づいて設定される確率です。主観確率を使用するため、人それぞれ違った確率になる場合もあります。

一方、頻度主義統計の確率は、ある出来事が長期的にどのくらいの頻度で起こるかという、客観的な頻度に基づいて定義されます。

観点	ベイズ統計	頻度統計
確率の意味	主観的：ある事象が起こる「信念の度合い」を表す。（例：「雨が降る確率は70%」→ 私の考えや情報に基づく推測）	客観的：繰り返し実験をしたときに、ある事象が起こる「長期的な頻度」を表す。（例：「雨が降る確率は70%」→ 実際に10回中7回雨が降る割合）

推論の方法

ベイズ統計では、パラメータ自体も確率変数として扱います。推定においては、事前の知識（事前分布）とデータから得られた情報（尤度）を組み合わせて、事後分布を計算します。この事後分布を使って、未知のパラメータの確率的性質を明らかにします。

一方頻度主義では、パラメータを固定の値とみなします。未知のパラメータに対して、データから推定値を得ることに焦点を当てます。

観点	ベイズ統計	頻度統計
考え方	過去の知識（事前確率）と新しいデータを組み合わせて推測を行う。	データ（サンプル）に基づいて推測を行う。事前の知識は使わない。
推論の手順	1. 事前確率（過去の知識）を設定する。 2. 新しいデータを基に事後確率を計算して更新する。	1. サンプルデータを使い、推定や仮説検定を行う。 2. 決まったルールで判断（p値や信頼区間など）。
計算に必要なもの	事前確率、新しいデータ、ベイズの定理。	サンプルデータ、統計モデル。

パラメータ

パラメータとは、母集団における平均値、割合、中央値、最大値、最小値、相関関係など、母集団の分布を特徴づける値のことです。

実用的な違い

ベイズ統計は、事前知識を反映できるため、小規模なデータセットや、事前にある程度の情報が得られている問題において有効です。

頻度主義統計は、特に大規模なデータセットにおいて、計算が比較的簡単で標準的な方法としてよく使用されます。データの数が多いほど、高精度の解析が可能になります。多くの伝統的な統計手法が、この方法に基づいています。

観点	ベイズ統計	頻度統計
柔軟性	柔軟に事前知識を反映できる。新しい情報が追加されるたびに確率を更新可能。	客観的なデータに基づいているため、誰がやっても同じ結果が得られる。
計算の負担	計算が複雑になることが多く、特にデータ量が多い場合はコンピュータの助けが必要。	比較的簡単な方法で計算できる。手計算でも可能な場合が多い。
利用される分野	医療、AI、機械学習など、過去の知識を活用する場面に適している。	科学研究、品質管理、社会調査など、実験データに基づく客観的判断が求められる場面に適している。

ベイズ統計の基本

ベイズ統計の根幹をなすのは、「ベイズの定理」と呼ばれる数学的な式です。ベイズの定理は、事前確率が尤度を受けて、どう変化するのかを示す事後確率を求めるための方法です。この定理を使うと、以前に得られた知識やデータを考慮して、新しいデータが与える情報を組み込みながら、確率を更新していくことができます。

尤度

尤度(ゆうど)とは、あるモデルや仮説のもとで観測されたデータが、どのくらい「もっともらしい」かを表すものです。

ベイズの定理

ベイズ統計の中心にあるのが「ベイズの定理」という公式です。

ベイズの定理 P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}

𝑃(𝐴∣𝐵): 事後確率（データ𝐵を基にした𝐴の確率）

𝑃(𝐴): 事前確率（データがないときの𝐴の確率）

𝑃(𝐵∣𝐴): 尤度（𝐴が起こった場合に𝐵が観測される確率）

𝑃(𝐵): 正規化定数（データ𝐵の確率）

ベイズの定理は、条件付き確率を扱うもので、ある仮説が真であるという確率を、新たなデータが与えられたときにどのように更新すべきかについて説明します。この原理は、新しい情報が得られるたびに先入観や以前のデータと組み合わせて確率を更新し、より情報に基づいた推論を可能にします。

事前確率と事後確率

事前確率（Prior Probability）は、データが与えられる前に持っている情報や予測に基づく確率です。

事後確率（Posterior Probability）は、観測データを基に更新された確率です。

例えば、朝出かける前に、あなたが財布を忘れる確率は 1% とします。これが事前確率です。

次に、お店に行ったとき、財布が見つかりませんでした。これは財布を忘れたかもしれないという新しい情報です。この新しい情報を基に、事後確率(財布を忘れた確率)が上がります。財布が見つからなかったことで、財布を忘れた確率が 50% に更新されるかもしれません。

客観確率と主観確率

客観確率は、繰り返し観察できる事象の長期的な傾向を基にした確率です。例として、コインを投げたときに表が出る確率は「1/2」です。これは実験を何度も繰り返して得られた客観的なデータに基づいており、誰もが同一の答えを導ける確率です。

一方、主観確率は、個人の知識や経験に基づいて判断される確率です。ベイズ統計の基礎となる考え方で、予測や信念に基づきます。例えば、スポーツの試合で「Aチームが勝つ確率は70%」と予想する場合、これはその人の知識や直感に基づく主観的な判断です。ベイズ統計では、主にこの主観確率を用います。

ベイズ統計の例

ここまでベイズ統計の基本概念などを解説してきましたが、この章では具体例と数値を用いて確率を実際に計算してみましょう！

例1　病気の診断

ある病気にかかる確率（事前確率）が 1%
ある病気にかかっている人が、検査で陽性と診断される確率が 96％
ある病気にかかっていない人が、検査で陽性と診断される確率が 2％

ある人の検査結果が陽性だった時、実際に病気にかかっている確率を求めよ。

今回は、病気にかかっている場合を事象A、陽性と診断される場合を事象Bとおきます。

ベイズの定理の定理から

P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} = \frac{P(A)P(B|A)}{P(A)P(B|A) + P(A^c)P(B|A^c)}

𝑃(𝐴)＝0.01　(ある病気にかかっている確率)

𝑃(𝐴^c)＝0.99 (ある病気にかかってない確率)

𝑃(𝐵∣𝐴)＝0.96　（ある病気にかかっており、検査で陽性となる確率）

𝑃(𝐵|𝐴^c)＝0.02（ある病気にかかっておらず、検査で陽性となる確率）

ここで、𝐴^cは、𝐴の余事象で、病気にかかってない事象を表します。

ベイズの定理の定理から

P(A|B) = \frac{0.01×0.96}{0.01×0.96 + 0.99×0.02)} = 0．326...

となります。したがって、検査結果が陽性の時、実際にある病気にかかっている確率は約33％です。

例2 迷惑メールの振り分け

すべてのメールのうち、迷惑メールである確率が10％
迷惑メールの中で、「再登録」という単語を含んでいる確率が30％
一般のメールの中で、「再登録」という単語を含んでいる確率が5％

メールの中で「再登録」という単語を含んでいた時、それが迷惑メールである確率を求めよ。

今回は、迷惑メールである場合を事象A、「再登録」という単語を含んでいる場合を事象Bとおきます。

ベイズの定理の定理から

P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} = \frac{P(A)P(B|A)}{P(A)P(B|A) + P(A^c)P(B|A^c)}

𝑃(𝐴)＝0.1　(迷惑メールである確率)

𝑃(𝐴^c)＝0.9 (迷惑メールではない確率)

𝑃(𝐵∣𝐴)＝0.3　（迷惑メールの中で「再登録」という単語を含んでいる確率）

𝑃(𝐵|𝐴^c)＝0.05（一般のメールの中で「再登録」という単語を含んでいる確率）

ベイズの定理の定理から

P(A|B) = \frac{0.1×0.3}{0.1×0.3 + 0.9×0.05)} = 0.4

となります。したがって、メールの中で「再登録」という単語を含んでいた時、それが迷惑メールである確率は、40％です。

ベイズ統計学のPythonでの実装

では、実際に簡単な実装を行ってみましょう。

このコードは、以下のような状況をシミュレートしています。

シナリオ: 製品の寿命についての予測を考えます。
事前には、「製品の寿命は平均50時間くらいだろう」と考えています（事前分布）。
実験データから「53時間程度」という新しい知見を得ました（尤度）。
この両方を統合し、製品の寿命の新しい予測を作成します（事後分布）。

# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# パラメータの設定
prior_mean = 50          # 事前分布の平均
prior_std = 10           # 事前分布の標準偏差
observed_mean = 53       # 観測されたデータの平均 (尤度の平均)
observed_std = 5         # 観測誤差の標準偏差 (尤度の標準偏差)

# 事後分布の計算
posterior_mean = (prior_mean / prior_std**2 + observed_mean / observed_std**2) / (1 / prior_std**2 + 1 / observed_std**2)
posterior_std = np.sqrt(1 / (1 / prior_std**2 + 1 / observed_std**2))

# x軸の範囲
x = np.linspace(30, 70, 500)

# 確率分布
prior_dist = norm.pdf(x, loc=prior_mean, scale=prior_std)
likelihood_dist = norm.pdf(x, loc=observed_mean, scale=observed_std)
posterior_dist = norm.pdf(x, loc=posterior_mean, scale=posterior_std)

# プロット
plt.figure(figsize=(10, 6))
plt.plot(x, prior_dist, label="事前分布 (Prior)", linestyle='--', color='blue')
plt.plot(x, likelihood_dist, label="尤度 (Likelihood)", linestyle='--', color='orange')
plt.plot(x, posterior_dist, label="事後分布 (Posterior)", color='red')
plt.title("ベイズ統計学: 事前分布、尤度、事後分布")
plt.xlabel("値")
plt.ylabel("確率密度")
plt.legend()
plt.grid(alpha=0.3)
plt.show()

# 結果の出力
print(f"事前分布: 平均={prior_mean}, 標準偏差={prior_std}")
print(f"尤度: 平均={observed_mean}, 標準偏差={observed_std}")
print(f"事後分布: 平均={posterior_mean:.2f}, 標準偏差={posterior_std:.2f}")

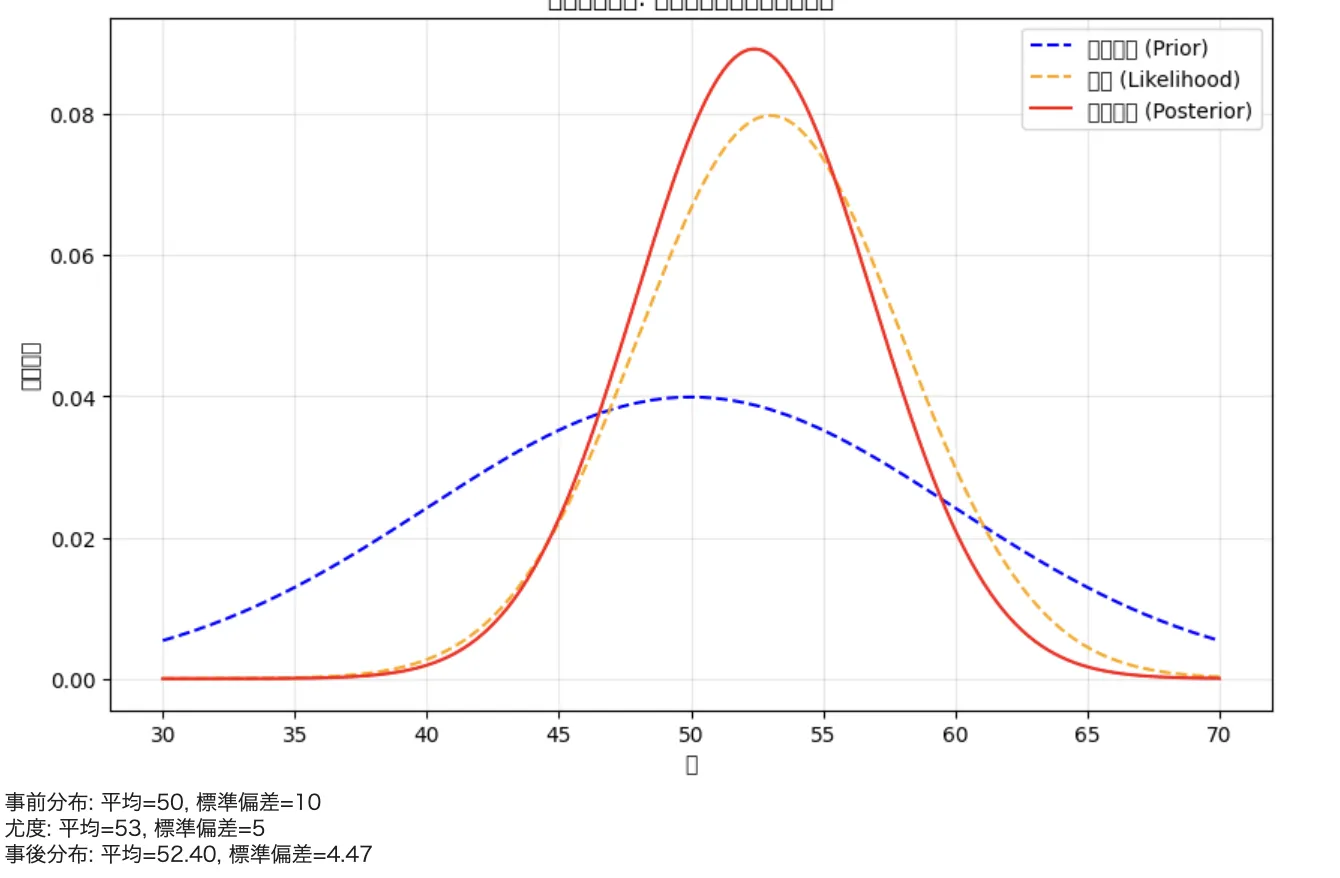
実行すると以下のような画像が出力されるはずです。

実行結果

事前分布 (青): 初期の予測。
尤度 (オレンジ): 新しいデータによる情報。
事後分布 (赤): 新しい情報を反映した最終的な予測。

ベイズ統計学の基本概念である「既存の知識を新しい情報でアップデートするプロセス」が実現されていますね。

ベイズ統計のメリット

ベイズ統計が持つ魅力的な特徴は、データの扱い方にあります。特に、「事前情報を活かして分析を進める」ことができる点や、少ないデータでも高い精度を発揮できる点は、大きな利点です。実際、日々の意思決定でも、過去の経験や知識をどう活かすかが重要になる場面が多いですよね。では、ベイズ統計がどのように私たちの意思決定に役立つのか、メリットを具体的に見ていきましょう。

事前情報を考慮できる

ベイズ統計は、既存の知識や信念を「事前確率」として考慮します。これにより、初期段階での仮定や専門的な知識を推論に取り込むことができます。たとえば、医療診断では、病気の既知の発生率を考慮した診断が可能です。

データが少ない場合にも強い

頻度主義的な統計手法は、十分な量のデータがなければ有効な推定が難しいのに対し、ベイズ統計では事前確率が補完するため、データが少ない場合でも信頼性のある推論が可能です。

データの更新が可能

ベイズ統計は、観測データが新たに得られるたびに確率を更新できます。つまり、事前確率に基づいて推定した結果が、追加データによりさらに正確な「事後確率」として更新されます。そのため、精度が高い確率を更新し続けることが可能です。

不確実性を明示的に扱える

ベイズ統計では、推定結果に対する不確実性を直接扱うため、モデルやパラメータに対する信頼性を直感的に理解できます。たとえば、「ある仮説が真である確率は80%」という形で表現できるため、意思決定者にとって分かりやすい結果を提供します。

柔軟性

ベイズ統計は、頻度主義的な統計では扱いにくい問題、例えば、非正規分布や異常値が見られるもの、データが少ない場合にも柔軟に対応できます。これにより、現実の複雑なデータや仮説にも適応しやすいのが強みです。

ベイズ統計のデメリット

一方で、ベイズ統計にもデメリットは存在します。特に、「事前確率の設定」や「計算の複雑さ」といった点が、実務で使う際に障壁となることがあります。ベイズ統計の利点を活かすためには、どのような注意点があるのか、見ていきましょう。

事前確率の設定が難しい

ベイズ統計では、事前確率を設定する必要がありますが、適切な事前確率を選ぶのが難しい場合があります。特に、事前知識が少ない場合は、その選択が結果に大きく影響を与える可能性があります。

また、事前確率は主観的な要素を含むため、分析者によって結果が異なる場合があります。これは、特に公平性が重要な場合に問題になることがあります。

そこで、非情報的事前分布（フラットな事前分布）を使うことで、事前知識が乏しい場合の主観性を減らせます。また、データに基づいて複数の事前確率を試し、結果が安定するか確認するのも有効です。

計算が複雑

データ量が増えると、ベイズ推論の計算が非常に複雑になり、特に多次元問題では計算負荷が高くなることがあります。

計算負荷を軽減するために、マルコフ連鎖モンテカルロ法（MCMC）や変分推論などの近似手法を用います。これにより、高次元の複雑な問題でも解が求めやすくなります。

大規模データに不向きな場合がある

ベイズ統計は、特に小規模データで強力ですが、大規模データでは頻度主義的なアプローチのほうが簡潔で効率的な場合があります。ベイズ統計では、すべてのデータに対して逐次的に事後確率を更新するため、計算時間が増加します。

変分ベイズ推論のような高速な近似法を使うことで、大規模データにも対応可能です。また、データをバッチに分割し、オンライン更新手法を採用することで処理速度を改善できます。

ベイズ統計の応用事例

ベイズ統計は医療、生態学、機械学習、マーケティング、金融など、多岐にわたる分野で応用されています。実世界の問題におけるベイズ統計の具体的な使用例から、そのメリットを理解しやすくするために、このセクションでは、異なる産業での実際の応用例を紹介します。

医療

ベイズ統計は、診断精度の向上に用いられます。たとえば、患者が特定の病気にかかる事前確率が1%だとし、検査結果が陽性ならば、ベイズの定理を使って病気にかかっている確率を再計算できます。これにより、検査結果に基づいてより精度の高い診断が可能です。

FDA（アメリカ食品医薬品局）

FDA（アメリカ食品医薬品局）は、ベイズ的手法を取り入れた「Complex Innovative Trial Designs」を推奨している。ベイズ統計を臨床試験に活用し、新薬開発を効率化させている。

FDA
引用元：PHARMA

生態学

生態学では、動物の個体数推定や絶滅リスクの評価にベイズ統計が使われます。観測データを基にして、個体数の減少傾向や環境変化に対する影響を事前確率として設定し、新たなデータを得ることで絶滅の可能性を再評価します。

アメリカの生態学者

例えば、アメリカの生態学者たちは、ベイズ統計を用いてフレッシュウォーターのムール貝3種の絶滅リスクを評価しました。これらの種のリスクは、都市開発や水文の変動が引き起こす環境の変化に基づいて計算され、今後の保存活動における意思決定に役立っていま。

ムール貝のフリー素材

機械学習

先述したように、GoogleやMicrosoftが提供するメールサービスでベイズ統計を活用したスパムフィルタリング技術が導入されています。これらの企業は、スパムメールの検出精度を高めるために、ベイズ統計に加え、自然言語処理や機械学習アルゴリズムを組み合わせて利用しています。

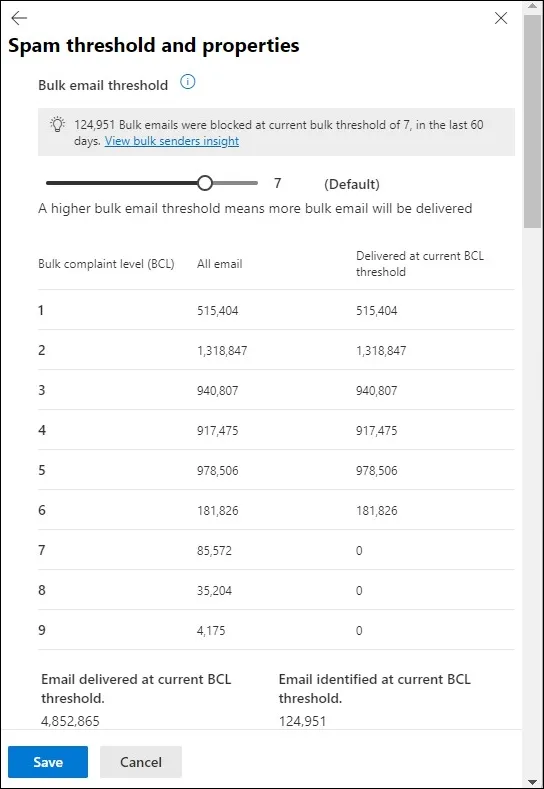
引用元：Microsoft

マーケティング

顧客が商品を購入する確率を事前に予測し、新しい購買データを使ってその確率を更新します。これにより、ターゲット広告の精度が向上し、マーケティング効果が高まります。

Infotools社

たとえば、Infotools社は、消費者データをベイズ的に解析して、人口統計や行動パターンの違いを可視化するツールを提供しています。この方法は、データの不確実性を考慮しつつ、特定の市場セグメントのプロファイルをより正確に理解するために役立っています。

金融

リスク管理や資産運用の分野でベイズ統計は重要です。過去の株式市場の動向を事前確率として設定し、最新の市場データに基づいてリスク評価を更新します。

まとめ

この記事を通じて、ベイズ統計の基本的な概念や原理、そしてその応用について解説しました。ベイズ統計は、事前の知識（事前分布）を元にデータから新たに得られた情報（尤度）を加味して、事後分布を更新する手法であり、主観的な確率を扱う柔軟なアプローチです。

ベイズ統計は、ただの数学的な手法ではありません。それは、過去の経験と新しい情報を結びつけ、私たちが未来に向けてより良い選択をするための道しるべです。このアプローチは、医療分野で命を救う新薬の開発を支え、マーケティングの世界で顧客の本質を理解する助けとなり、さらには検索エンジンやAI技術の根幹を成すものとして私たちの日常にも深く関わっています。

その強みは、確率という形で不確実性を明確に捉える点にあります。データが曖昧であっても、それを否定するのではなく、受け入れて次の一歩を導き出す力。それがベイズ統計の真髄です。これからもこの考え方が、技術の進化とともに新たな発見や発展を生み出していくことでしょう。そして、その進化の中で、私たちはデータという言葉に込められた『可能性』を再発見するのかもしれません。