教師なし学習とは？その仕組みや教師あり学習との違い、実装方法を解説

教師なし学習は、正解ラベルなしのデータから隠れたパターンや構造を発見する機械学習の手法です。クラスタリング・次元削減・異常検知など、ラベル付けコストをかけずにデータの価値を引き出せる点が特徴です。
本記事では、教師あり学習との違い、代表的なアルゴリズム（k-means、PCA、t-SNE）、Google Colabでの実装手順、実際の活用事例を解説します。

教師なし学習とは？

教師なし学習とは、正解ラベル（出力データ）が与えられないデータ（入力データ）のみを用いて、データに潜むパターンや構造を学習する機械学習の手法です。
教師あり学習のように「問題」と「解答」のセットは用いず、データそのものから有用な情報を抽出します。

例えば、大量の顧客データから似たような属性や行動パターンを持つ顧客グループを見つけ出したり、文章データからトピックを抽出したりすることが、教師なし学習の典型的な応用例です。

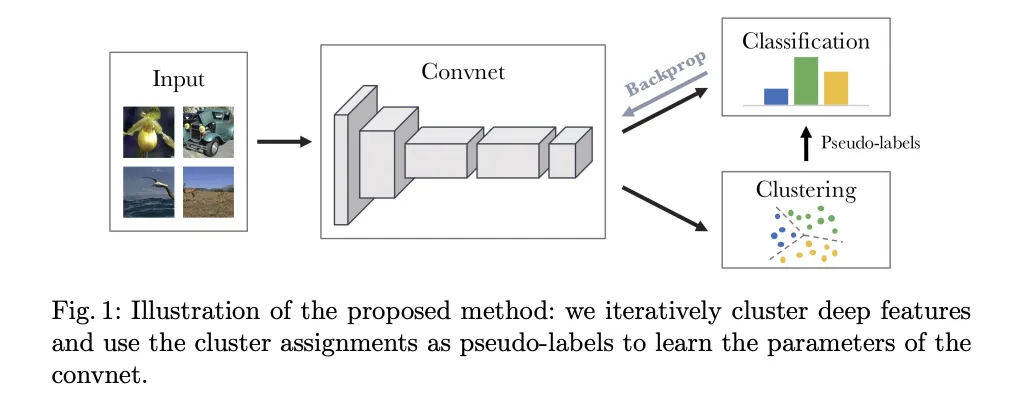
教師なし学習の考え方　参照：論文

教師あり学習との違い

教師あり学習と教師なし学習の最も大きな違いは、正解ラベルの有無です。教師あり学習では、入力データとそれに対応する正解ラベルをセットで学習させることで、予測モデルを構築します。

一方、教師なし学習では、正解ラベルを用いずに、データ間の類似性や関係性に基づいて、データの分類や特徴抽出を行います。

この表からもわかるように、教師あり学習は「正解」を予測することを目的としているのに対し、教師なし学習はデータそのものの理解を深めることを目的としていると言えます。

教師なし学習のメリット

教師なし学習には、教師あり学習をはじめとする他の手法にはないいくつかのメリットがあります。ここでは、教師なし学習の主なメリットを解説します。

ラベルなしデータを活用できる

現実世界では、正解ラベルが付与されたデータは限られており、ラベルなしデータの方が圧倒的に多く存在します。
教師なし学習では、このようなラベルなしデータを有効活用できるため、データ収集のコストを削減できます。

ラベル付け作業は、時間と労力を要する作業であり、特に大量のデータに対しては大きな負担となります。教師なし学習は、この負担を軽減し、より多くのデータから価値を引き出すことを可能にします。

未知のパターンを発見できる

教師なし学習は、データに潜む未知のパターンや構造を発見するのに適しています。
例えば、顧客の購買履歴データから、これまで気づかれていなかったような購買パターンを発見したり、遺伝子データから新しい疾患のメカニズムを発見したりといったことが可能になります。

人間が事前に想定していないような、新しい知見が得られる可能性を秘めているのです。

データの構造を理解できる

教師なし学習を用いることで、データの構造や特徴をより深く理解できます。
これは、データ分析や、より効果的な特徴量の設計に役立ちます。

例えば、次元削減によってデータを可視化することで、データの分布や特徴を直感的に把握したり、クラスタリングによってデータ間の類似性や相違点を明らかにしたりできます。

教師なし学習のデメリット

教師なし学習は強力な手法ですが、いくつかのデメリットも存在します。ここでは、そのデメリットについて説明し、それを克服するためのアプローチについて考察します。

結果の解釈が難しい

教師なし学習では、出力結果が必ずしも人間にとって理解しやすい形であるとは限りません。
例えば、クラスタリングによってデータが複数のグループに分けられたとしても、そのグループが何を意味するのかを解釈するのは人間です。

多くの場合、結果の解釈には、対象分野に関する専門知識や経験が必要となります。

適切な評価が難しい

教師なし学習では、正解ラベルが存在しないため、学習結果の良し悪しを客観的に評価するのが難しい場合があります。
評価指標の選択や、結果の妥当性の検証には、専門的な知識や経験が必要となります。

例えば、クラスタリングの評価には、シルエット係数やダン指数などの指標が用いられますが、どの指標が最適かは、データやタスクによって異なります。

アルゴリズムの選択が重要

教師なし学習には様々なアルゴリズムが存在し、それぞれ異なる特性を持っています。
タスクやデータに応じて適切なアルゴリズムを選択することが重要であり、そのためには、各アルゴリズムの仕組みや特徴を理解しておく必要があります。

例えば、データが線形分離可能な場合は主成分分析が有効ですが、非線形な構造を持つデータにはt-SNEの方が適している場合があります。

教師なし学習の種類と代表的なアルゴリズム

教師なし学習には、大きく分けて「クラスタリング」「次元削減」「異常検知」など、様々なアルゴリズムが存在します。ここでは、その中でも特に代表的なアルゴリズムについて、その仕組みや特徴を解説します。

その他の手法についても以下の記事で詳しく解説しています。
機械学習の代表的な手法一覧！フローチャートを用いて選び方を解説

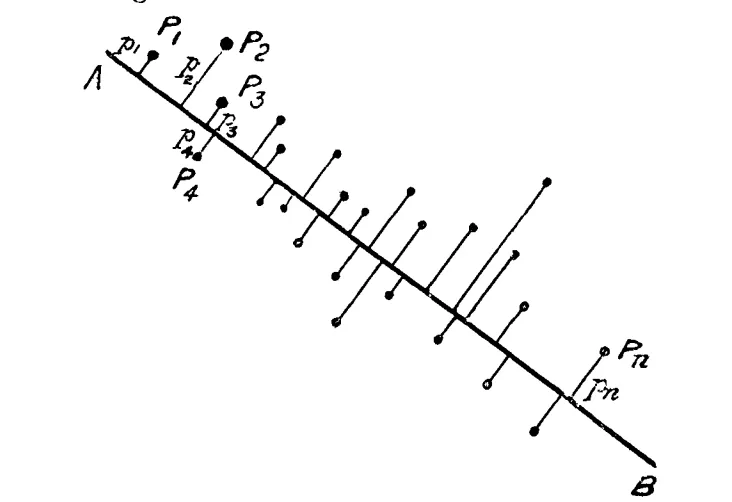
PCAの考え方の基礎となった概念　参照：論文

クラスタリング - データをグループ化

クラスタリングとは、データ間の類似度に基づいて、データを複数のグループ（クラスタ）に分割する手法です。
例えば、顧客データをクラスタリングすることで、似たような購買行動を示す顧客グループを発見し、マーケティング戦略の立案に役立ちます。

他にも、文書の自動分類や、画像の領域分割など、様々な応用例があります。

k-means法（k-means clustering）

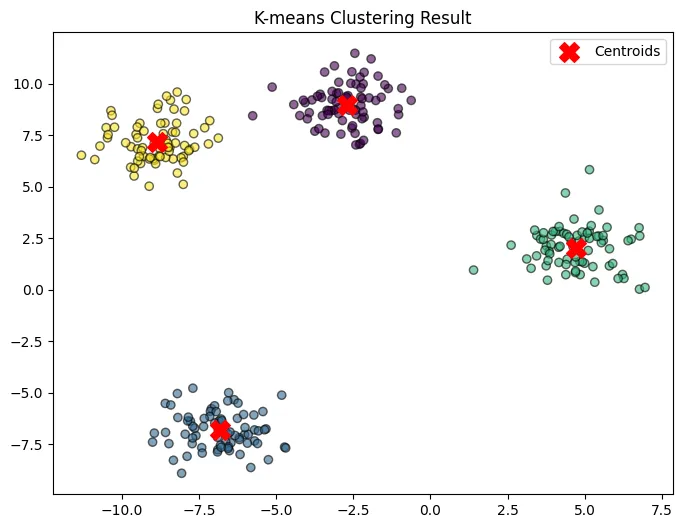
k-meansを使って作成した画像
k-means法は、クラスタリングの代表的なアルゴリズムの一つです。データを予め決められたk個のクラスタに分割します。

各クラスタは重心と呼ばれる点で代表され、各データ点はいずれかの重心に最も近いクラスタに割り当てられます。

手順:

1. k個の重心をランダムに初期配置する
2. 各データ点を、最も近い重心に割り当てる
3. 各クラスタの重心を、そのクラスタに属するデータ点の平均位置に更新する
4. 上記ステップ2と3を、重心の位置が変化しなくなるまで繰り返す

シンプルで高速なアルゴリズムですが、初期値依存性や、クラスタ数が事前に決定されている必要がある点に注意が必要です。

階層的クラスタリング（Hierarchical Clustering）

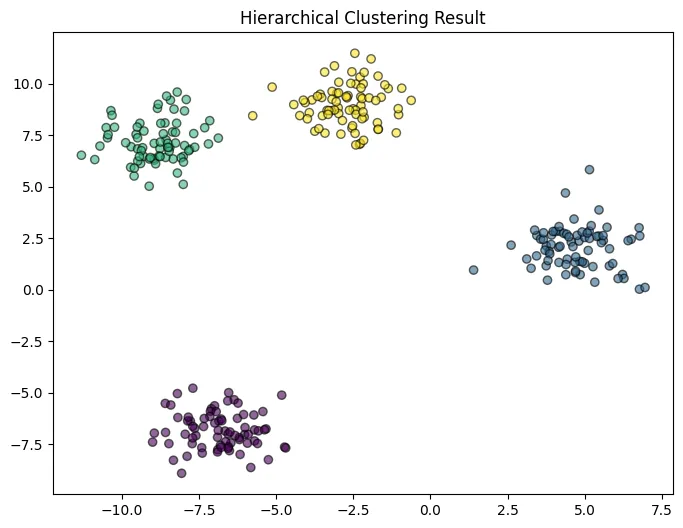
階層的クラスタリングによって作成された画像
階層的クラスタリングは、データ点間の距離に基づいて、データ点を階層的にクラスタにまとめていく手法です。
樹形図（デンドログラム）を用いてクラスタリングの結果を可視化できるため、クラスタ数の決定や結果の解釈に役立ちます。

手順:

1. 各データ点を個別のクラスタとする
2. 最も距離が近い2つのクラスタを併合する
3. 上記ステップ2を、クラスタが1つになるまで繰り返す

階層的クラスタリングには、クラスタ間の距離の定義によって、最短距離法、最長距離法、群平均法などのバリエーションがあります。

次元削減 - データの次元を減らす

次元削減とは、データの持つ情報をなるべく損なわずに、データの次元数を減らす手法です。
高次元データを低次元空間に圧縮することで、データの可視化や、計算コストの削減、過学習の抑制などに効果があります。

例えば、数百次元の画像データを2次元や3次元に圧縮することで、人間が視覚的に理解しやすくなります。また、機械学習モデルの前処理として次元削減を行うことで、モデルの学習時間短縮や精度向上に繋がる場合もあります。

主成分分析（PCA）

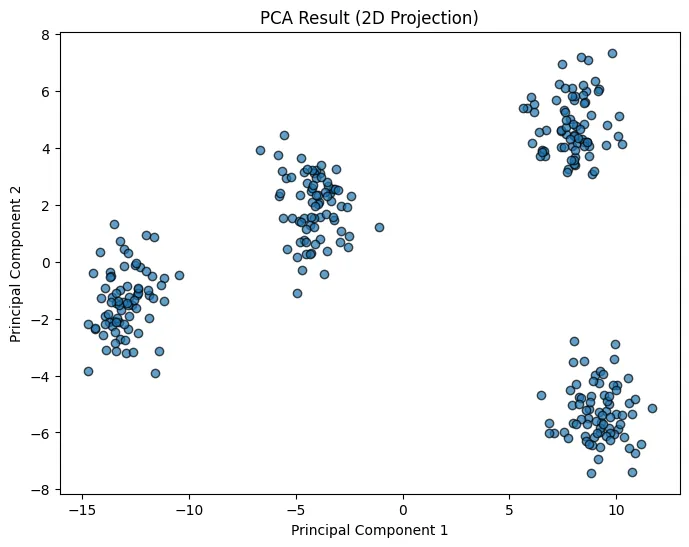
主成分分析を用いて作成した画像
主成分分析（PCA）は、次元削減の代表的な手法の一つです。
データの分散が最大となる方向（主成分）を順次見つけていくことで、元のデータの特徴をなるべく保持したまま、データの次元を削減します。

手順:

1. データの共分散行列を計算する
2. 共分散行列の固有値と固有ベクトルを求める
3. 固有値が大きい順に固有ベクトルを並べ、主成分とする
4. データを主成分で構成される空間に射影する

データの可視化や、特徴量の抽出などに用いられます。

t-SNE（t-distributed Stochastic Neighbor Embedding）

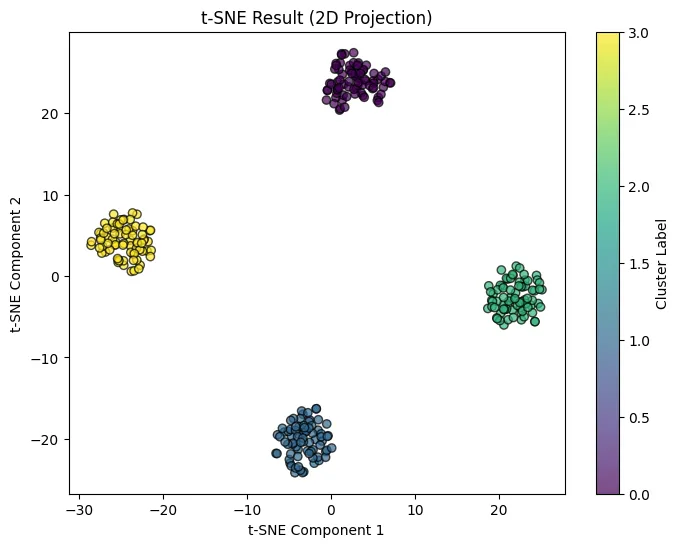
t-SNEを用いて作成した画像
t-SNEは、主に高次元データの可視化に用いられる次元削減手法です。
データ点間の類似度を確率分布で表現し、高次元空間と低次元空間の確率分布がなるべく一致するように、データ点を低次元空間に配置します。
t-SNEは、局所的な構造を保持しつつ、データを低次元空間に埋め込めるため、高次元データの可視化に非常に有効です。

アソシエーション分析 - 関連ルールを抽出

アソシエーション分析とは、大量のデータから項目間の関連ルールを見つけ出す手法です。

アプリオリアルゴリズム（Apriori Algorithm）

アソシエーション分析で頻出アイテム集合を見つけるためのアルゴリズムです。

例えば、スーパーマーケットの購買データから、一緒に購入されることが多い商品の組み合わせを発見する際に使われます。
アプリオリアルゴリズムは、「頻出アイテム集合の全ての部分集合は頻出である」という性質を利用して、効率的に頻出アイテム集合を見つけ出します。

異常検知 - 通常とは異なるデータを見つける

異常検知とは、データセットの中から、通常とは異なるパターンを示すデータ（外れ値）を検出する手法です。製造ラインの異常検知や、クレジットカードの不正利用検知などに用いられます。例えば、正常な製品のデータから特徴を学習し、その特徴から大きく外れたデータを異常と判断する、といった方法があります。

自己符号化器（Autoencoder）

自己符号化器は、ニューラルネットワークを用いた次元削減手法の一つです。
入力データを一度低次元の表現に変換（エンコード）した後、元のデータを復元（デコード）するように学習を行います。
この過程で、データの本質的な特徴を抽出できます。自己符号化器は、画像のノイズ除去や、特徴抽出などに用いられます。

教師なし学習の実装手順（Google Colab）

教師なし学習はお手元で簡単に実装できます。
Pythonの機械学習ライブラリ（例: scikit-learn）を使用すれば、データのクラスタリングや次元削減を簡単に実行できます。
ここでは Google Colaboratory を用いて、K-means クラスタリング を実装します。

最終的に完成したコードは以下のトグルに示しています。

ここからは、実装手順をステップバイステップで具体的な出力例と合わせて解説します。

!pip install -q numpy pandas scikit-learn matplotlib

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# データを生成（3つのクラスターを持つ2次元データ）
X, y = make_blobs(n_samples=300, centers=3, cluster_std=1.0, random_state=42)

# データの散布図を描画
plt.scatter(X[:, 0], X[:, 1], s=30)
plt.title("Generated Data for Clustering")
plt.show()

# K-means モデルを作成（K=3に設定）
kmeans = KMeans(n_clusters=3, random_state=42)

# モデルをデータに適用（クラスタを学習）
kmeans.fit(X)

# 予測されたクラスタラベルを取得
labels = kmeans.predict(X)

# 各クラスタの中心を取得
centers = kmeans.cluster_centers_

# クラスタごとに異なる色でデータをプロット
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=30, alpha=0.6)

# クラスタの中心を赤でプロット
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, label='Centroids')

plt.title("K-means Clustering Result")
plt.legend()
plt.show()

print("クラスタの中心座標:")
print(centers)

print("\n最初の10個のデータ点のクラスタラベル:")
print(labels[:10])

inertia = []
K_range = range(1, 10)

for k in K_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    inertia.append(kmeans.inertia_)

plt.plot(K_range, inertia, marker='o')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal K')
plt.show()

ステップ 1: Colab 環境の準備

Google Colab を開き、新しいノートブックを作成します。
以下のコードを入力して実行してください。

# 必要なライブラリをインストール（Colabでは通常不要）
!pip install -q numpy pandas scikit-learn matplotlib

このコマンドは、Colab 環境にすでにあるライブラリを更新する際に役立ちます。

ステップ 2: 必要なライブラリのインポート

以下のコードを Colab に入力して、実行してください。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

ステップ 3: データセットの生成

教師なし学習では、データのラベル（正解）が与えられないため、データの構造を自動的に発見する必要があります。
ここでは、make_blobs() を使って 3つのクラスタ を持つ擬似データを生成します。

# データを生成（3つのクラスターを持つ2次元データ）
X, y = make_blobs(n_samples=300, centers=3, cluster_std=1.0, random_state=42)

# データの散布図を描画
plt.scatter(X[:, 0], X[:, 1], s=30)
plt.title("Generated Data for Clustering")
plt.show()

✅ 予想される出力例

• 300個のデータ点がランダムに分布した散布図
• 3つの中心点（クラスタ）を持つように配置されている

ステップ 4: K-means クラスタリングを適用

K-meansクラスタリングを適用し、データを3つのグループに分類します。

# K-means モデルを作成（K=3に設定）
kmeans = KMeans(n_clusters=3, random_state=42)

# モデルをデータに適用（クラスタを学習）
kmeans.fit(X)

# 予測されたクラスタラベルを取得
labels = kmeans.predict(X)

# 各クラスタの中心を取得
centers = kmeans.cluster_centers_

ステップ 5: クラスタリング結果を可視化

クラスタリングの結果をプロットして、分類されたデータを確認します。

# クラスタごとに異なる色でデータをプロット
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=30, alpha=0.6)

# クラスタの中心を赤でプロット
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, label='Centroids')

plt.title("K-means Clustering Result")
plt.legend()
plt.show()

✅ 予想される出力例

• 3つのクラスタに異なる色がつけられた散布図
• クラスタの中心（Centroids）が赤いXマークで表示される

ステップ 6: クラスタリングの結果を確認

クラスタの中心座標や、どのデータがどのクラスタに属しているかを表示します。

print("クラスタの中心座標:")
print(centers)

print("\n最初の10個のデータ点のクラスタラベル:")
print(labels[:10])

✅ 予想される出力例

クラスタの中心座標:
[[-2.63323268  9.04356978]
 [-6.88387179 -6.98398415]
 [ 4.74710337  2.01059427]]

最初の10個のデータ点のクラスタラベル:
[1 1 0 2 1 2 0 2 0 0]

ステップ 7: クラスタ数Kの最適値を決定（エルボー法）

クラスタ数 (K) の選択は重要です。
エルボー法を使って最適な (K) を求める方法を紹介します。

inertia = []
K_range = range(1, 10)

for k in K_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    inertia.append(kmeans.inertia_)

plt.plot(K_range, inertia, marker='o')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal K')
plt.show()

✅ 予想される出力例

• エルボー法のグラフ
• K=3あたりで「ひじ」のように曲がるポイントがあり、最適なクラスタ数を示す

✅ 各ステップのまとめ

これでK-means の基本的な使い方が理解できるはずです。
異なるクラスタ数（K=4, 5, 6 など）を試したり、他のデータセットで実験したりすることで、理解がさらに深まります。

教師なし学習の活用事例

教師なし学習は、様々な分野で実際に活用されています。
ここでは、その具体的な活用事例を紹介し、教師なし学習がどのように社会に貢献しているかを明らかにします。

各事例について、実際に活用されているサービスや関連情報のリンクも掲載しています。

顧客セグメンテーション

顧客の購買履歴や属性などのデータを用いて、顧客をいくつかのグループに分類します。
これにより、各グループの特性に合わせたマーケティング戦略を立案することが可能になります。
例えば、年齢、性別、購買履歴などの情報から、顧客を「20代女性、ファッションに関心が高い」「30代男性、ビジネス書をよく購入する」といったグループに分類し、それぞれのグループに最適な商品やサービスを提案できます。

活用事例

• Google Analytics（GA4）：ユーザーの行動をクラスタリングし、セグメントごとに分析
  🔗 Google Analytics
• Salesforce Customer 360：AIによる顧客データの統合・分析
  🔗 Salesforce Customer 360

レコメンデーション

ユーザーの行動履歴や嗜好などのデータを用いて、ユーザーが興味を持ちそうな商品やサービスを推薦します。
ECサイトや動画配信サービスなどで広く活用されています。

例えば、Amazonでは、ユーザーの購買履歴や閲覧履歴から、そのユーザーが興味を持ちそうな商品を推薦しています。Netflixでは、ユーザーの視聴履歴から、好みに合いそうな映画やドラマを推薦しています。

活用事例

• Amazonの「おすすめ商品」：購入履歴や閲覧履歴を基に最適な商品を推薦
  🔗 Amazon公式サイト
• Netflixのコンテンツ推薦システム：視聴履歴を分析し、類似したコンテンツを推薦
  🔗 Netflix
• Spotifyの「Discover Weekly」：音楽の嗜好を分析し、新しい楽曲を推薦
  🔗 Spotify

画像圧縮

画像データをより少ない情報量で表現することで、データサイズを削減します。
これにより、ストレージ容量の節約や、データ転送時間の短縮に繋がります。例えば、JPEGなどの画像フォーマットでは、主成分分析などの技術を用いて、画像データを圧縮しています。

活用事例

• JPEG圧縮：DCT（離散コサイン変換）を用いた画像圧縮
  🔗 JPEG圧縮の技術解説
• Google Photosの画像圧縮：機械学習による圧縮最適化
  🔗 Google Photos
• TinyPNG：スマートな画像圧縮サービス（PNG・JPEG対応）
  🔗 TinyPNG

異常検知

製造ラインのセンサーデータや、クレジットカードの利用履歴などから、通常とは異なるパターンを検出します。
これにより、製品の不良や不正利用を早期に発見できます。例えば、工場のセンサーデータから、製品の異常な振動や温度上昇を検知したり、クレジットカードの不正利用を検知したりできます。

活用事例

• Visaの不正検知システム：AIによるリアルタイム不正決済検出
  🔗 VisaのAI活用事例
• AWS Fraud Detector：機械学習を活用した不正検知
  🔗 AWS Fraud Detector
• GE Predix（製造業向け異常検知）：IoTデータを活用した異常検知
  🔗 GE Predix

テキストマイニング

大量のテキストデータから、有用な情報を抽出します。
例えば、SNSの投稿を分析することで、世の中のトレンドや、特定の製品に対する消費者の意見を把握できます。
また、ニュース記事をクラスタリングすることで、似たような内容の記事を自動的にグループ化したり、トピックを抽出したりすることもできます。

活用事例

• Google Trends：検索ワードの傾向を分析
  🔗 Google Trends
• Twitter API（X）：SNSの投稿データを収集・分析
  🔗 Twitter API
• IBM Watson Natural Language Understanding：企業向けの高度なテキスト分析
  🔗 IBM Watson NLU

教師なし学習は、さまざまな分野で実用化されており、ビジネスや日常生活に大きな影響を与えています。
各技術を活用することで、効率的なデータ分析や最適な意思決定が可能になります。

データ分析のAI知見を組織全体の業務改革へ

ラベルなしデータからパターンを発見する教師なし学習の考え方は、業務データの中から改善ポイントを見出すAI導入設計にも直結します。クラスタリングや次元削減で培った分析力を、組織全体のAI業務自動化にどう展開するかが次のステップです。

AI総合研究所では、Microsoft環境での段階的なAI業務自動化を220ページの実践ガイドにまとめています。AI総合研究所の専任チームが、データ分析の知見を全社的なAI導入計画に接続するところまで支援します。まずはガイドで、自社に合った段階的導入の進め方をご確認ください。

データ分析のAI知見を組織全体の業務改革へ

パターン発見から業務プロセス設計へ

ラベルなしデータからパターンを見出す力を、組織全体のAI業務設計に展開しませんか。Microsoft環境での段階的導入を220ページの実践ガイドで解説しています。

▶ 無料でダウンロード

まとめ

教師なし学習には、大きく3つの価値があります。

1つ目は、正解ラベルなしのデータから隠れたパターンや構造を発見できる点です。ラベル付けコストをかけずに、顧客セグメンテーションや異常検知など実務に直結する知見を得られます。

2つ目は、クラスタリング・次元削減・アソシエーション分析など、目的に応じた多様なアルゴリズムを選択できる点です。k-meansで顧客グループを発見し、PCAで高次元データを可視化し、Autoencoderで異常を検知するといった使い分けが可能です。

3つ目は、教師あり学習の前処理としても機能し、特徴量設計やデータ理解を通じて機械学習パイプライン全体の精度向上に貢献できる点です。

まずはGoogle Colabで本記事のk-meansクラスタリングのコードを実行し、クラスタ数やパラメータを変えて出力の変化を確認してください。自社データに適用する際は、エルボー法で最適なクラスタ数を決定してから本格的な分析に移行するアプローチが有効です。

【参考文献】
Caron, M., Bojanowski, P., Joulin, A., & Douze, M. (2018): Deep Clustering for Unsupervised Learning of Visual Features
🔗 論文リンク

• 教師なし学習における特徴学習のための手法「DeepCluster」を提案。畳み込みニューラルネットワークの特徴をクラスタリングし、擬似ラベルを生成して学習を強化する反復プロセスを導入。ImageNetなどのデータセットで評価し、教師あり学習と比較しても競争力のある結果を示した。

Pearson, K. (1901): On Lines and Planes of Closest Fit to Systems of Points in Space
🔗 論文リンク

• データの分散を最大化する直線や平面を求める手法として、主成分分析（PCA）の基礎を確立した論文。多次元空間内の点群を最もよく近似する直線や平面の数学的定式化を行い、現代の統計学および機械学習における次元削減手法の礎を築いた。