この記事のポイント
この記事は機械学習の回帰分析に関する解説を行っています。
回帰分析はデータ間の関係性をモデル化し、未来の連続値を予測するための手法です。

Microsoft MVP・AIパートナー。LinkX Japan株式会社 代表取締役。東京工業大学大学院にて自然言語処理・金融工学を研究。NHK放送技術研究所でAI・ブロックチェーンの研究開発に従事し、国際学会・ジャーナルでの発表多数。経営情報学会 優秀賞受賞。シンガポールでWeb3企業を創業後、現在は企業向けAI導入・DX推進を支援。
機械学習における回帰分析は、連続する数値の予測に用いられる重要な手法です。データの関係性をモデル化し、未来の予測などに利用するこの手法の基本から応用までを、本記事ではわかりやすく解説していきます。線形から非線形、単回帰から重回帰に至るまで、各手法の特徴を具体的な例と共に紹介。また、Pythonを使った実践的な回帰分析の方法や、ビジネスでの活用事例についても触れます。データに隠されたパターンを読み解き、的確な意思決定を支援する回帰分析の実力を、ぜひこの機会に身につけてください。
目次
機械学習における回帰分析とは
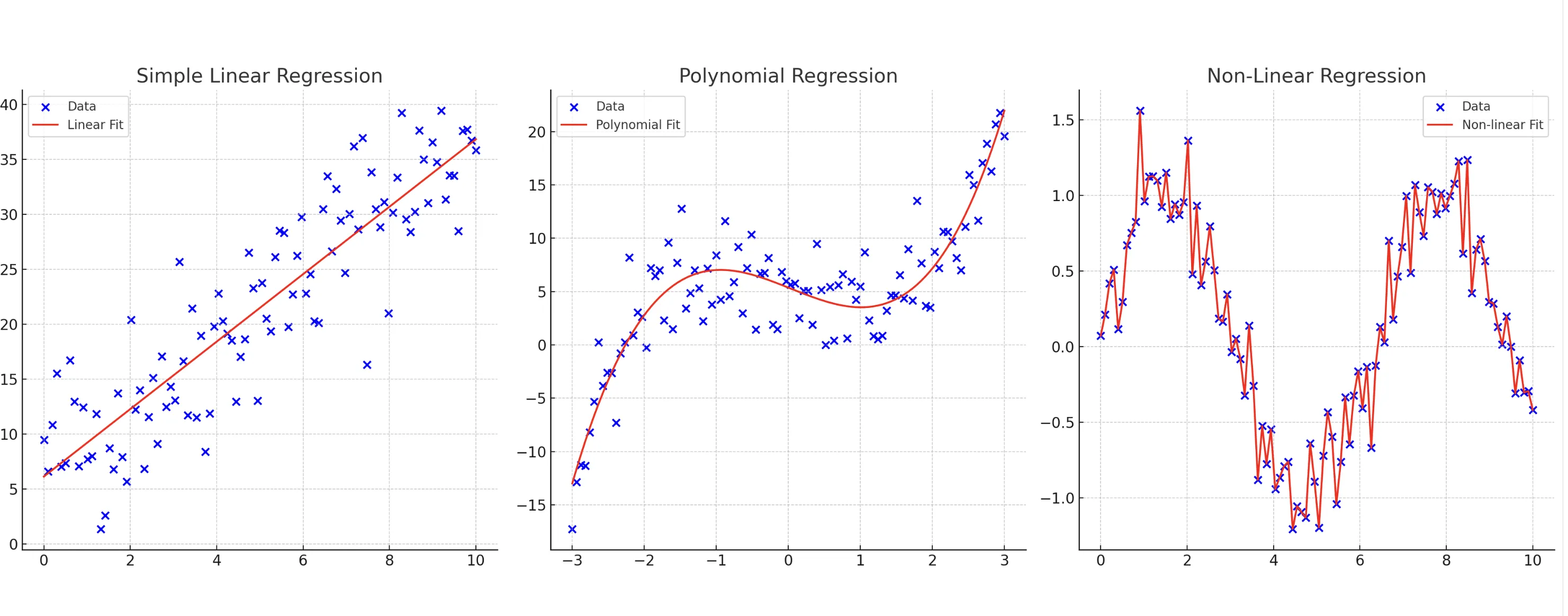
回帰分析の主要な手法
まず回帰とは、連続する入力値に対する次の値を予測することです。
機械学習での「回帰分析」は、入力データと出力データの関係をモデル化し、未来を(連続的な数値データを)予測するための手法です。
上記の画像は回帰分析の主要な手法を図示したものです。
直線のものもあれば、曲線、線形でないものもあるでしょう。
このようにさまざまなタイプのデータをモデル化し、データの傾向やパターンを把握し、新しいデータに基づいた予測や意思決定をサポートします。
回帰分析の従属変数と独立変数
回帰分析とは、従属変数(予測対象)と独立変数(説明要因) との間の関係を数理モデルで表現する手法です。
少し難しく聞こえますが観測データに基づき、関数形式のモデルを構築することで、次のようなことを予測します。
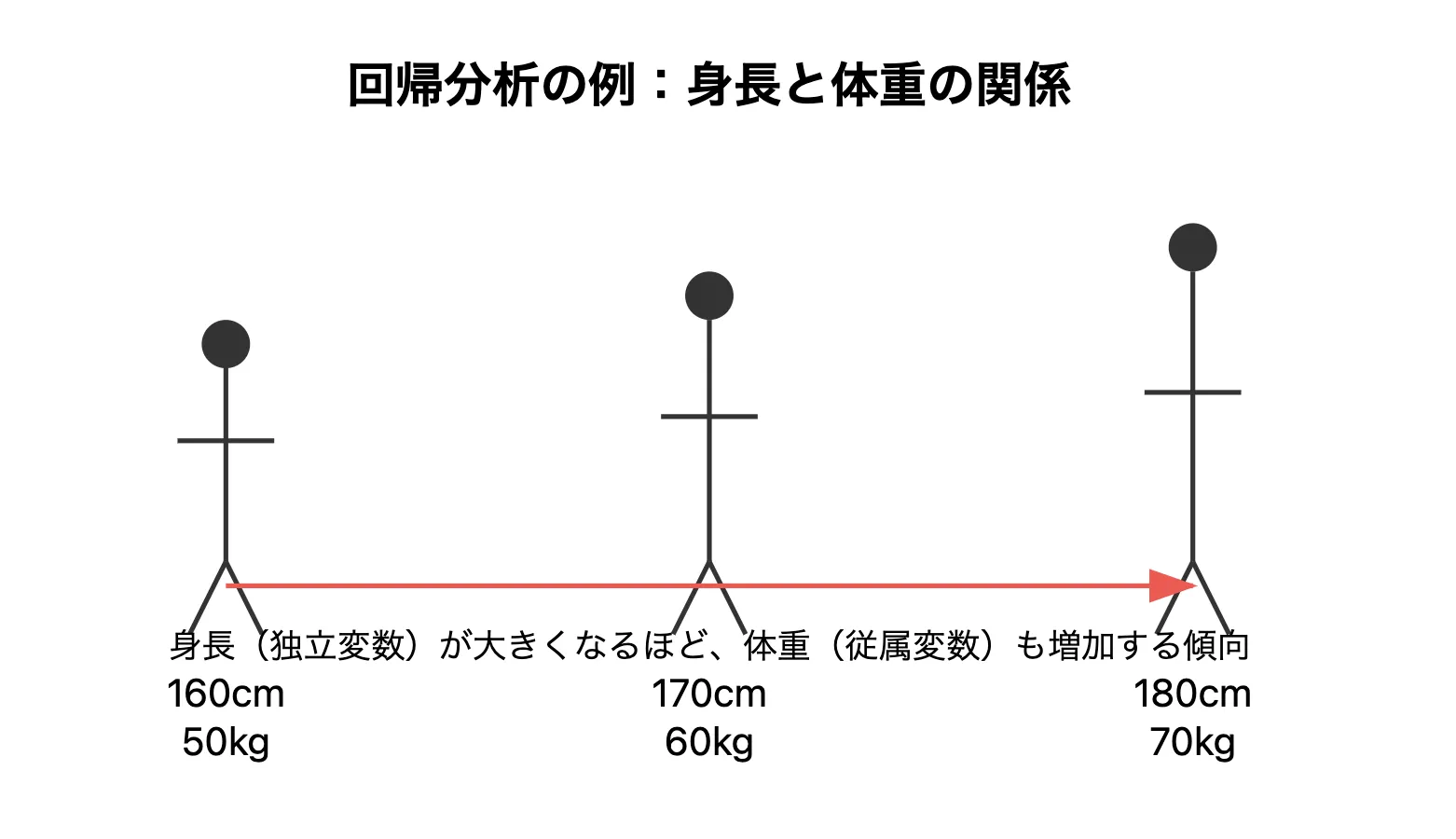
従属変数と独立変数のイメージ
この画像は身長が高くなることに体重も増加することを図示したものです。
- 独立変数(説明要因) - 身長であり、予測に使用する要因
- 従属変数(予測対象) - 体重であり、予測したい対象
この関係性により、身長が高くなるにつれて、体重も増加する傾向がわかるかと思います。
この関係を数式で表現するのが回帰分析です。
回帰分析の目的
では、回帰分析はどのような場面で使用されるのでしょうか。
以下に使用の目的のシーンをまとめました。
| 目的 | 説明 | 例 |
|---|---|---|
| 関係性の把握 | 独立変数が従属変数にどのような影響を与えるかを定量的に理解する | 気温がアイスクリームの売上に与える影響 |
| 予測 | モデルを用いて新しいデータに基づく従属変数の値を予測する | 次月の売上や株価の予測 |
| シナリオ分析 | 独立変数を変化させた場合の従属変数の変化をシミュレーション | 広告予算を増加させた場合の売上増加試算 |
| 異常値やパターンの発見 | モデルと大きく異なる観測値を特定し、異常や重要なパターンを発見する | 工業生産における異常値の検出 |
回帰分析と分類の違い
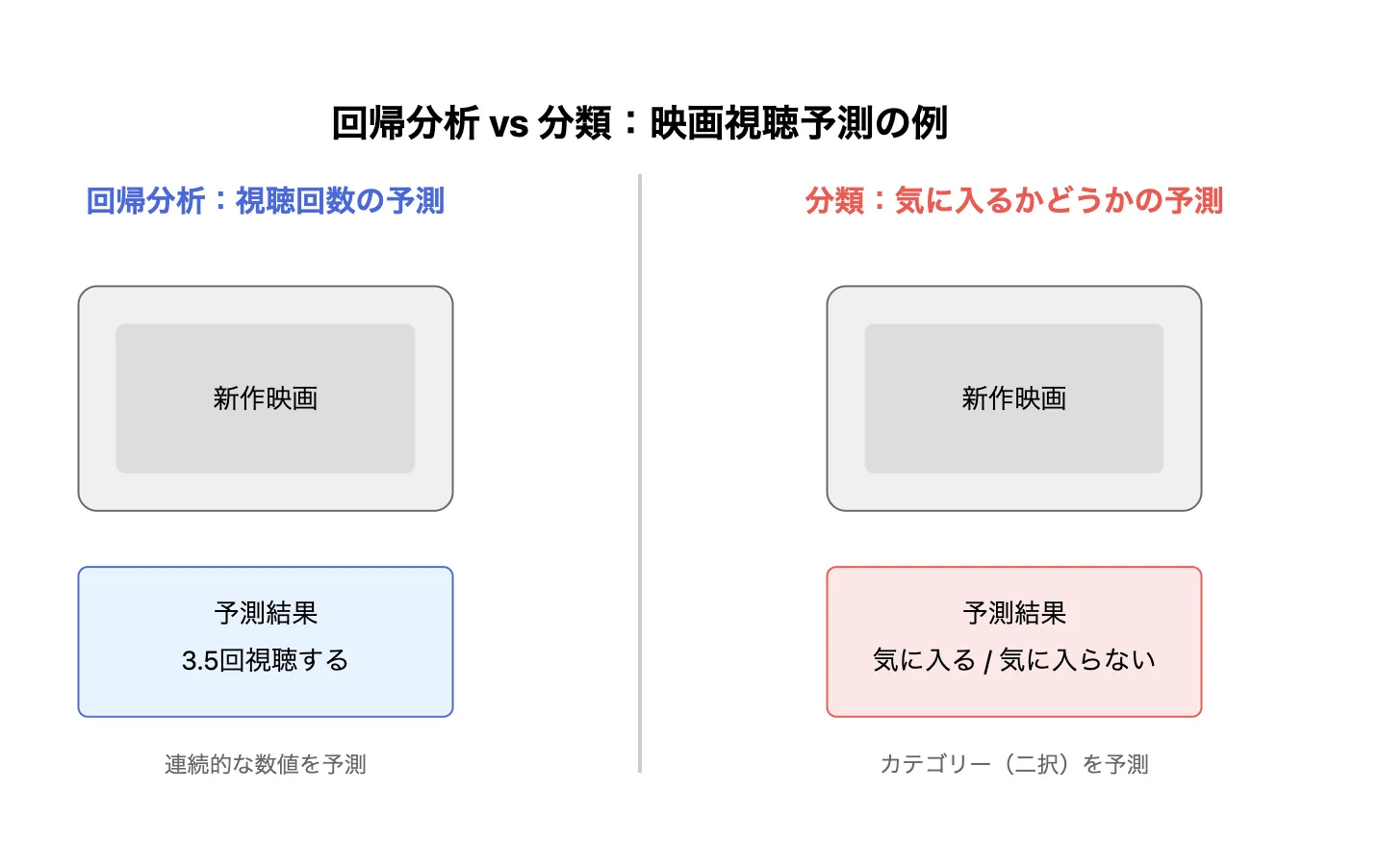
回帰分析と分類の違い
勘違いされることもあるのですが、回帰分析と分類は同じではありません。
以下に違いを説明します。
- 出力の性質:回帰分析では連続値。分類では離散値。
- 適用範囲:回帰は数値予測に特化しデータの傾向やパターンを学習する。分類はクラスの識別に特化しデータをグループ分けする。
- アルゴリズム:回帰では主に線形回帰や決定木回帰。分類ではロジスティック回帰、サポートベクターマシーンなどを利用。
分類は回帰と同じように次の値を予測できるモデルですが、分析できるデータの性質が異なります。
例えば、回帰分析で過去の視聴履歴を基に、顧客が新しく配信された映画を「何回視聴するか」を予測します。しかし分類では、過去の視聴履歴を基に、顧客が新しく配信された映画を「気に入るかどうか」(二択)を予測します。
回帰分析結果の解釈方法
回帰分析の結果を解釈するためには、主に以下の要素を確認します。
| 項目 | 意味 | 解釈例 | 注意点 |
|---|---|---|---|
| 回帰係数(傾き) | 各独立変数が従属変数に与える影響を示す | 広告費が1万円増えると売上が2万円増加する | 大きさと符号の意味を理解する |
| 切片(定数項) | 全ての独立変数がゼロのときの従属変数の値を示す | 広告をしない場合でも売上が50万円ある | 実務では参考程度にする |
| モデルの適合度(R²値) | モデルが従属変数の分散をどれだけ説明できるかを示す | R²=0.85の場合、モデルが85%の分散を説明できる | 高すぎるR²は過剰適合の可能性 |
| p値(有意性の検定) | 各独立変数の影響が統計的に有意かを検定する | p<0.05なら独立変数の影響が有意である | 有意でない変数を再検討する |
| 残差(予測値と実測値の差) | モデルがどれだけ正確に予測できたかを測る指標 | 残差が小さいほど予測精度が高い | 残差がランダムでない場合はモデル改善が必要 |
回帰分析の結果を正確に解釈することで、ビジネス上の意思決定や戦略策定に直接つなげることができます。分析の目的やデータの背景を考慮しながら、これらの要素を確認することが重要です。
回帰分析の種類と手法
機械学習における回帰分析にはさまざまな種類があり、それぞれ異なる方法でデータを解析します。ここででは、代表的な手法を具体的な例や数式を用いて解説します。
全体の手法の特徴と比較
各種回帰分析のグラフを作成し、それぞれの特徴と違いを表にまとめました。
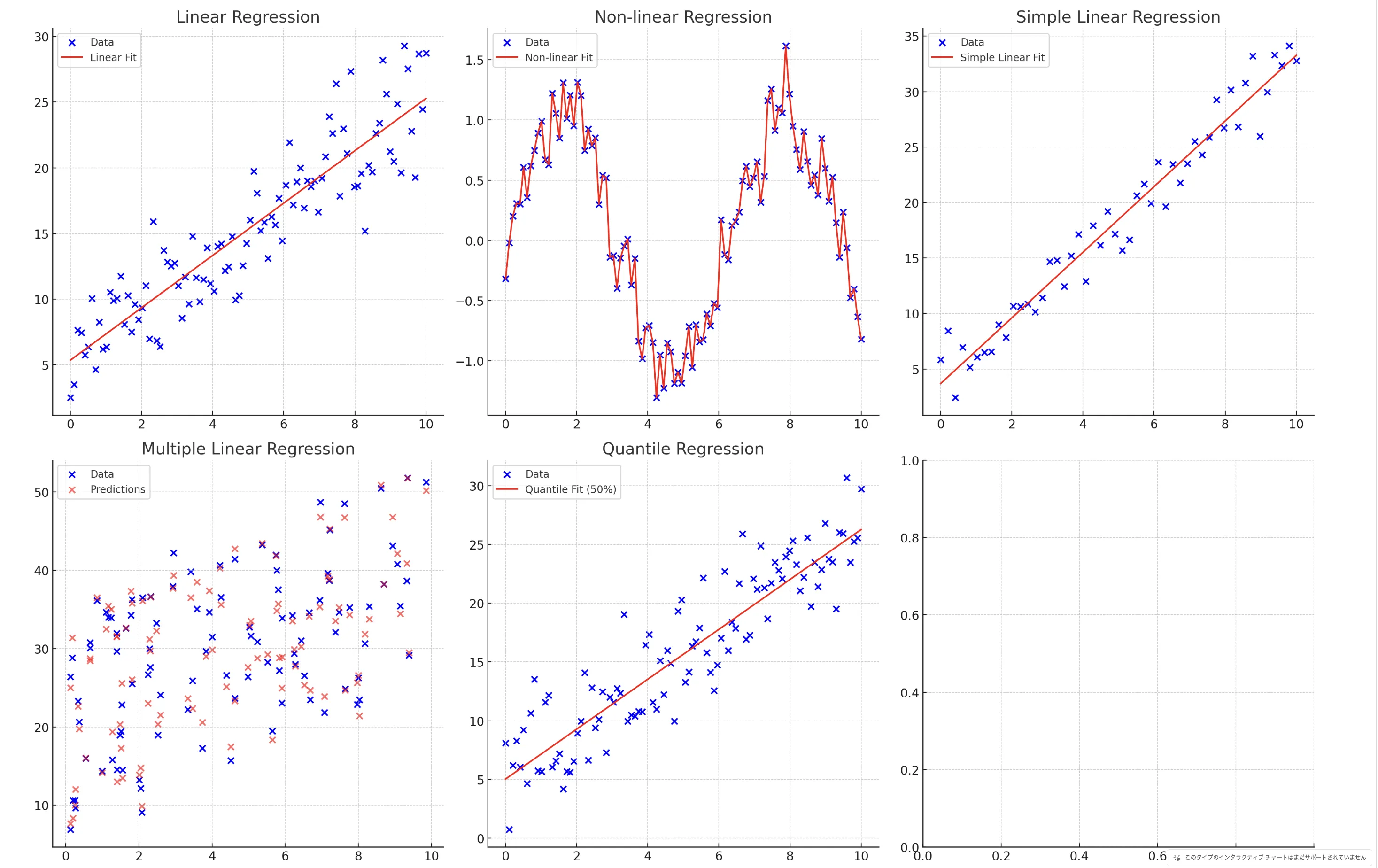
回帰分析の手法と特徴
| 回帰の種類 | 特徴 | 例 | 図の位置 |
|---|---|---|---|
| 線形回帰分析 | 従属変数と独立変数が直線的関係にある場合の回帰分析 | 身長と体重の関係のモデル化 | 左上 (Linear Regression) |
| 非線形回帰分析 | データのパターンが非線形である場合の回帰分析 | 株価の周期的な変動のモデル化 | 上中央 (Non-linear Regression) |
| 単回帰分析 | 独立変数が1つだけの場合の回帰分析 | 広告費と売上の関係を分析 | 右上 (Simple Linear Regression) |
| 重回帰分析 | 複数の独立変数を用いて従属変数を予測する回帰分析 | 広告費や気温が売上に与える影響を分析 | 左下 (Multiple Linear Regression) |
| 分位点回帰分析 | 特定の分位点(例:中央値)を予測する回帰分析 | 所得の中央値を予測するモデル | 下中央 (Quantile Regression) |
以下では、各手法の説明と実際の計算手順を紹介します。
線形回帰の実際の計算手順
線形回帰は、説明変数と目的変数との間の線形関係をモデル化する回帰手法の一つです。
線形回帰の一般的なモデルは次の形を取ります。
- ( y ): 目的変数(予測したい値)
- ( x ): 説明変数(入力値)
- ( β0): 切片(回帰直線が縦軸と交わる点)
- ( β1 ): 傾き(説明変数が1単位増加するごとの目的変数の変化量)
- ( ε ): 誤差項(実際の値と予測値の差)
線形回帰の具体的な求め方
- 1.データを用意して具体的な線形モデルを立てる
ここでは、住宅価格を線形回帰を用いて予測してみようと思います。データの例として以下の表の数値を用います。
| 面積(平方メートル) | 価格(万円) |
|---|---|
| 50 | 250 |
| 80 | 400 |
| 100 | 500 |
| 120 | 600 |
住宅価格を面積で予測する線形関数は、以下のようになります。
-
(y):価格
-
(x):面積
-
2.データに基づくパラメータを推定する。
具体的にこのデータを用いて説明変数 ((x)) と目的変数 ((y)) の平均を計算します。
次にβ1を計算します。最小二乗法を用いて以下の一般式に各テータの数値と計算した値を代入します。
結果の以下のようになります。
最後にβ0を計算します。以下の式に求めた数値を代入します。
結果は以下のようになります。
得られた回帰モデルは次の通りです
- 3.得られた回帰モデルを利用して予測する。
ここでは、面積90の価格を予測してみます。
$$
\bar{価格}=240.625+2.25×90=443.125
$$
また、この線形関数をグラフにすると任意の予想値が線形直線上で示されます。
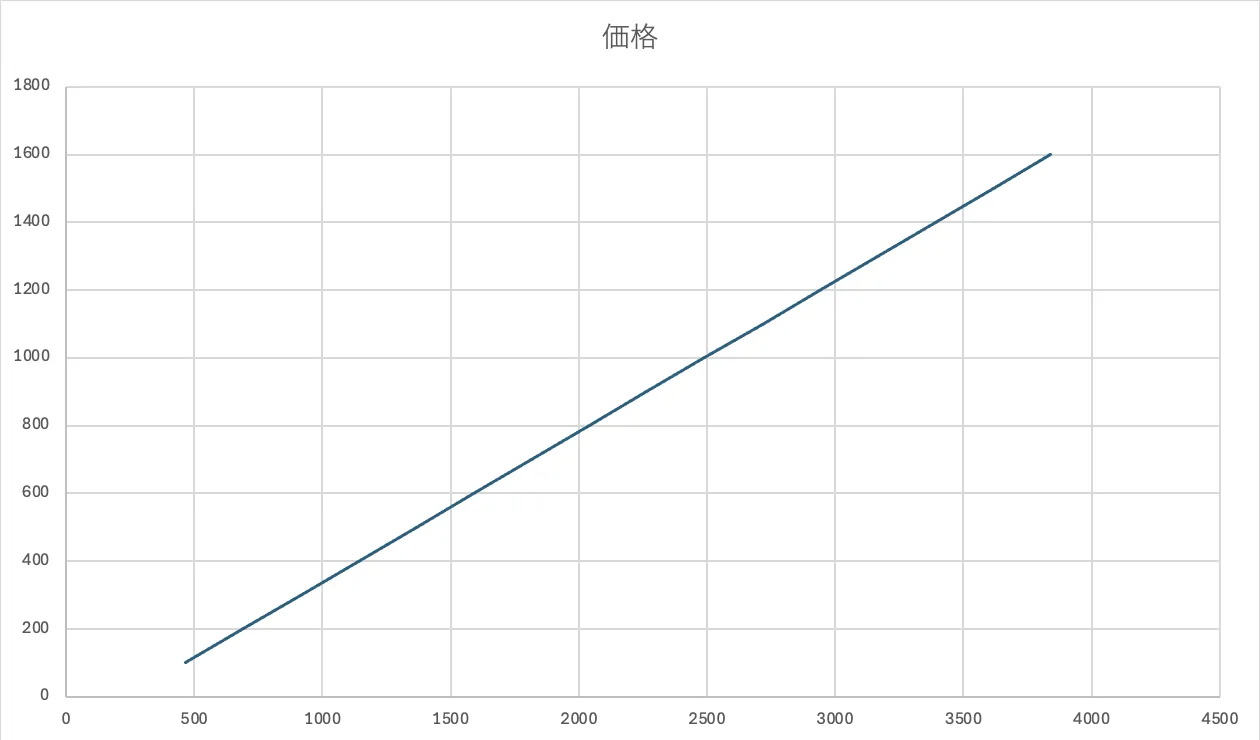
非線形回帰の実際の計算手順
非線形回帰は、説明変数と目的変数の間に非線形な関係が存在する場合に使用される手法です。非線形の関係とは、データが直線的なパターンではなく曲線的な関係を表します。
具体的な非線形回帰の例として以下のような数式があります。
ここで、
- ( θ0, θ1, θ2 ): モデルのパラメータ(回帰係数)
- ( f(x;\θ) ): 目的変数((x) に依存する非線形関数)
非線形回帰のパラメータ推定は線形回帰の場合と異なり、以下のような手法を利用します。
- 1.最急降下法(Gradient Descent)
損失関数 L(θ)の勾配を計算し、パラメータを更新します:
- 2.最小二乗法の数値解法
より複雑な非線形モデルでは、以下の方法を使用することがあります:
- 勾配ベースの数値解法。
- ライブラリ(例えば Scipy の
curve_fit関数)。
非線形回帰の具体的な例
具体的な非線形回帰を利用する例として気象データの予測が挙げられます。具体的には、地表温度や降水量が日照時間や温度に依存する非線形関係を持ちます。この非線形回帰のモデルとしては、2次多項式モデルが利用されることが多いです。
日照時間と温度の関係を表すモデルの例:
- T: 温度
- x: 日照時間
- (θ0,θ1,θ2):パラメータ
単回帰分析
単回帰分析は、1つの説明変数が1つの目的変数に与える影響を分析します. 単回帰分析の基本的な例としては、この記事の線形回帰分析で例に挙げた一次関数のモデルがあります。
また、非線形の単回帰分析も存在します。その例として学習時間と試験スコアなどが挙げられます。学習時間が増えるとそれに応じて試験スコアは伸びますが、一定以上勉強時間が増えると点数の向上は鈍化します。この場合は単純な一次関数でデータのパターンは表すことができません。こうした事例では非線形回帰を利用します。
非線形単回帰をモデルとして選択する理由としては、線形モデルが不十分な場合以外に、データの現実的な挙動を自然に反映するためでもあります。
重回帰分析の実際の計算手順
重回帰分析は、複数の説明変数が目的変数に与える影響を同時に考慮します。重回帰分析の一般的な数式は以下のようになります。
- ( y ): 目的変数(例: 住宅価格)
- ( x1, x2, x3 ): 説明変数(例: 敷地面積、部屋数、築年数)
- ( β0 ): 切片(すべての説明変数がゼロのときの予測値)
- ( β1, β2, β3 ): 回帰係数(各説明変数の目的変数への影響度)
- ( ε ): 誤差項(モデルが説明しきれない部分)
重回帰分析の具体的な例
重回帰分析の具体的な例として住宅価格を例にしてみます。データを以下のように設定します。
| 敷地面積 ((x1)) | 部屋数 ((x2)) | 築年数 ((x3)) | 住宅価格 ((y)) |
|---|---|---|---|
| 100 | 3 | 5 | 3000 |
| 120 | 4 | 10 | 3200 |
| 80 | 2 | 20 | 2000 |
| 150 | 5 | 3 | 4000 |
次に重回帰分析の回帰係数を求めます。
重回帰分析で回帰係数が(β0,β1,β2,β3)=(1000,15,300,-50)と仮にすると、モデルは次のようになります。
目的変数を予測します
敷地面積:100,部屋数3,築年数5の住宅価格を予測すると、モデルに説明変数を代入して結果として3150万円と予測できます。
重回帰分析における複数変数の選択
重回帰分析において、モデルの説明変数を全て利用するとは限りません。目的変数に最も近づけるために説明変数を選択する必要があります。そこで、説明変数を選択するために利用する方法があります。
- 部分回帰:複数の説明変数がある場合に、特定の変数が目的変数に与える独立した影響を明らかにするための手法
- AIC:モデルの適合度と複雑さのバランスを評価するための指標。AICは、モデルの予測精度を高める一方で、過剰なパラメータを避けるためにペナルティを与える。
分位点回帰の実際の計算手順
分位点回帰は、データの特定の分位点(中央値や四分位点など)に基づいて回帰モデルを作成します。応答変数全体を分析するので、異常値の影響を避けながら、偏りのあるデータの傾向を分析したい場合に有用です。
通常の回帰分析が説明変数で条件付けた目的変数の条件付き期待値を扱うが、分位点回帰は、説明変数で条件付けた目的変数の条件付き分位点を扱います。分位点とは、データをある規則に基づいて並べたときに、特定の割合でデータを分割する位置を示す値のことで、代表的なものとしてデータの中央値が挙げられます。さらに、分位点回帰の目的は、分布全体のモデリング、ロバストな推定が可能、不均一な影響の分析などのようになります。
分位点回帰分析での課題としては、着目する分位点ごとにモデルを構築するための計算コストが高くなってしまう可能性があることや、結果の解釈がしやすい線形回帰分析と比較して解釈が難しいことが挙げられます。また、データによっては、特定の分位点においてデータ量が少ないと分位点回帰分析の結果の推定が不安定になってしまいます。
分位点回帰の一般的な数式は次のようになります。
- ( y_i ): 応答変数(目的変数)
- ( \mathbf{x}_i ): 説明変数のベクトル
- ( \beta ): 回帰係数のベクトル
- ( q ): 分位点(0 < ( q ) < 1)
ここで、損失関数は次のように定義されます:
分位点回帰の具体的な例
賃金の分布分析
- 目的:労働の賃金に影響を与える要因を分析
- 分位点回帰の利点:分位点回帰では、賃金分布の下位層や上位層への影響を個別に分析できる。この事例に線形回帰を用いると、教育や経験が平均賃金に与える影響を分析することができるが、特定の着目したい層の分析はすることができない。
回帰分析の実践時のチェックポイント
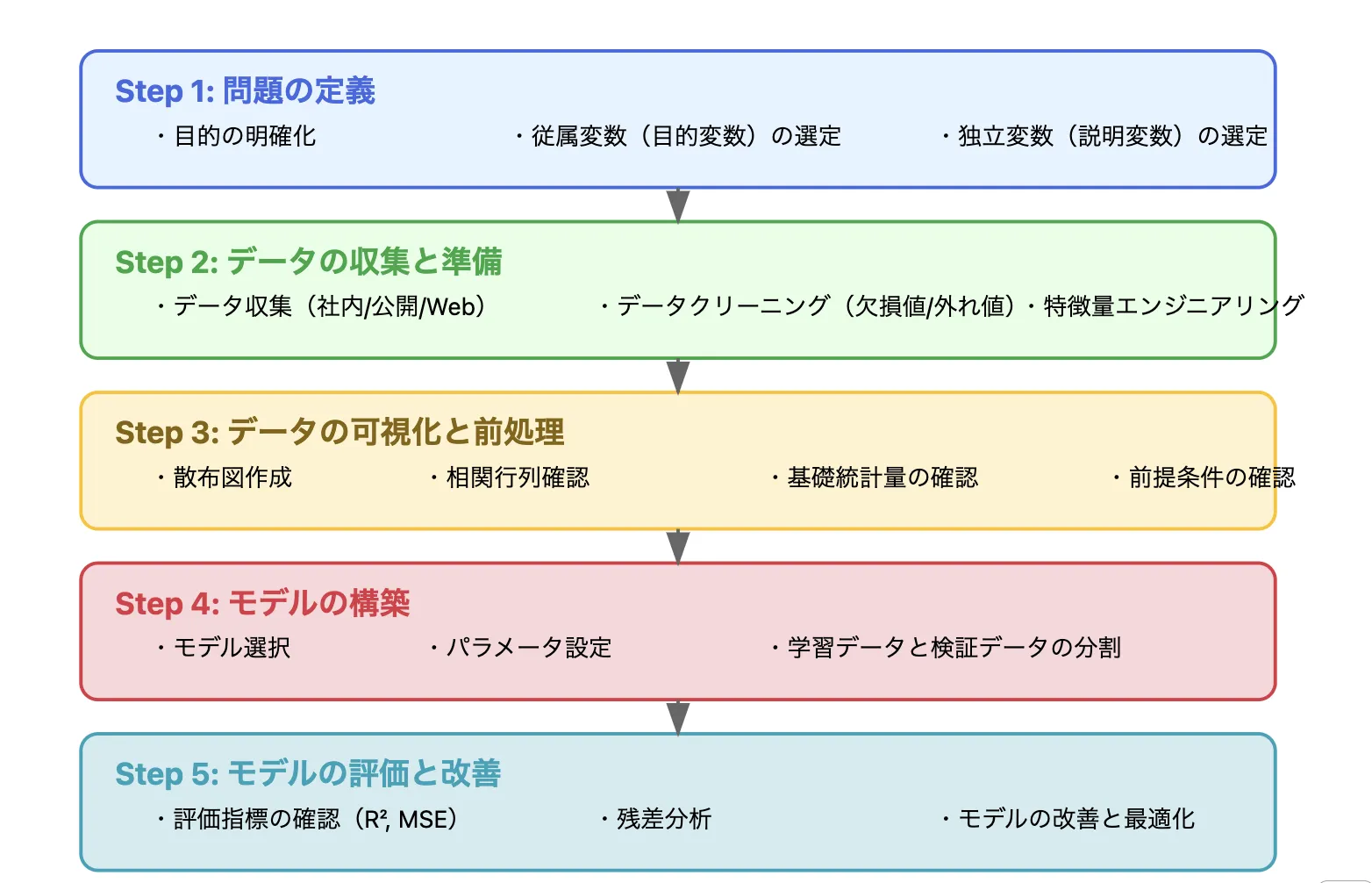
回帰分析の実践時のチェックポイント
回帰分析を実際に行う際には、回帰分析モデルの選択の他にも様々なことを決定し考える必要があります。ここでは、実際にビジネスに回帰分析を応用するときに必要なことを手順を追って紹介していきます。
1.問題の定義
まず、回帰分析を利用する目的を明確に決める必要があります。回帰分析を利用することがより効果的となる目的を定めることが回帰分析を実際にビジネスに応用する際に重要です。回帰分析を利用して何を予測・理解したいのかを明確化したら、次に(目的変数)従属変数と(説明変数)独立変数を選定します。
2.データの収集と準備
回帰分析の元となるデータを収集します。収集先としては、社内データ、公開データ、Webスクレイピングなどを利用します。データを収集したらデータのクリーニングが必要です。データに欠損値や外れ値があると回帰分析に影響を出すので事前に処理が必要となります。また、複数のデータを用いる場合データの型の確認と必要に応じた変換が必要になります。
目的変数をより理解しやすくさせるために特徴量エンジニアリングをします。特徴量エンジニアリングでは、カテゴリ変数のダミー変数化や数値変数の標準化・正規化、必要に応じて新たな特徴量を生成します。
3.データの可視化と前処理
変数間の関係性を理解しやすくするために散文図や相関行列を作成してデータを可視化します。可視化されたデータを元にして前提条件を確認します。
4.モデルの構築
上記の準備ができたらデータと分析目的に最も適したモデルを選定します。回帰分析の種類と手法のセクションで紹介した回帰分析のほかに以下のようなモデルもあります。
- リッジ回帰
- ロジスティック回帰
- ランダムフォレスト回帰
様々な回帰分析モデルの中から利用するモデルを選びます。
モデルを選定したら、モデルの構築をします。モデルは、PythonやR、Excelを用いて回帰式を構築しデータに適合させます。
5.モデルの評価と改善
回帰分析に用いるモデルを選定したらモデルの評価と改善をします。
モデルの具体的な評価としては*評価指標の計算,残差分析,過学習の確認などがあります。
モデルの評価をしたときにモデルの改善が必要な場合非線形モデルを考慮したり、パラメータを調整したり、不要な変数の削除や新たな特徴量を作成して改善します。
Pythonを用いた回帰分析の実践
Pythonは、機械学習と回帰分析のための強力なツールを提供しています。以下に、Pythonを使用した回帰分析の基本的なプロセスを示します。
1. Pythonでの回帰分析のステップ
-
データの準備
- 必要なライブラリ(
numpy,pandas,matplotlib,sklearn)をインポート。 - データを収集・クレンジングし、分析に適した形式に変換。
- 必要なライブラリ(
-
モデルの選択
- 線形回帰 (
LinearRegression) - 非線形回帰 (
PolynomialFeatures,GaussianProcessRegressor) - 分位点回帰 (
QuantileRegressor)
- 線形回帰 (
-
モデルのトレーニング
- データセットをトレーニングデータとテストデータに分割。
- モデルを適合(
fit)させて係数を学習。
-
評価と可視化
- モデルの予測精度を評価(
R²やRMSE)。 - グラフで実際のデータと予測値を比較。
- モデルの予測精度を評価(
-
予測の応用
- 新しいデータを用いて、従属変数(予測値)を推定。
2. 実践例
では実際にコードを使ってみましょう。
以下をコピペしてもらえたらGoogleコラボなどでもすぐ実装が可能です。
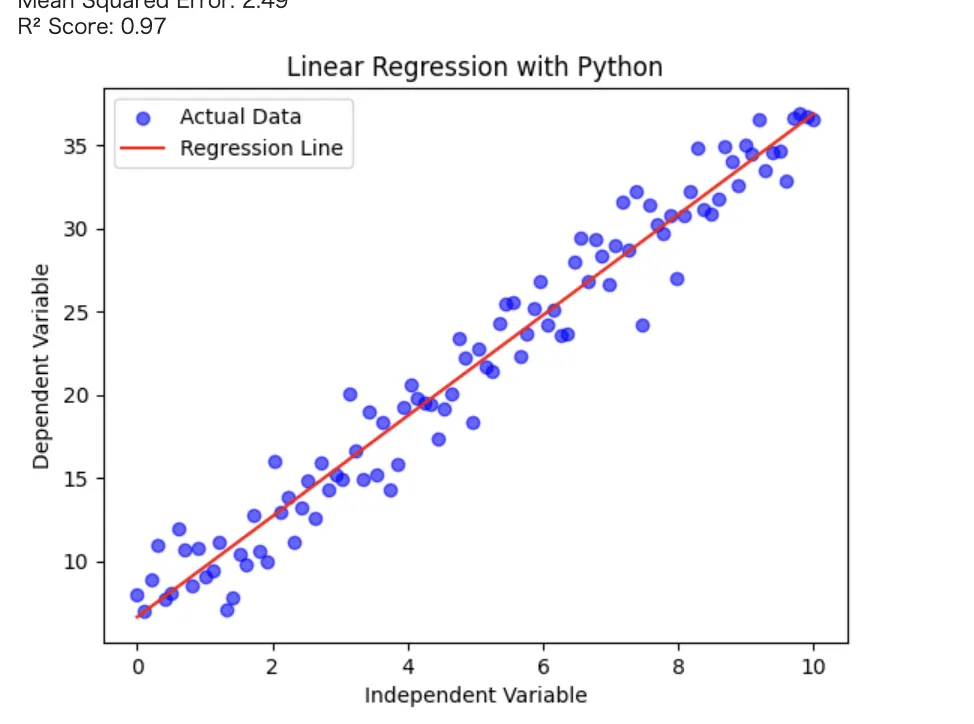
実行結果
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの生成
np.random.seed(42)
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel() + 7 + np.random.normal(scale=2, size=100)
# トレーニングとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 線形回帰モデルの構築
model = LinearRegression()
model.fit(X_train, y_train)
# 予測と評価
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
# 結果の表示
print(f"Mean Squared Error: {mse:.2f}")
print(f"R² Score: {r2:.2f}")
# グラフの描画
plt.scatter(X, y, label="Actual Data", color="blue", alpha=0.6)
plt.plot(X, model.predict(X), label="Regression Line", color="red")
plt.title("Linear Regression with Python")
plt.xlabel("Independent Variable")
plt.ylabel("Dependent Variable")
plt.legend()
plt.show()
Python以外のツールのご紹介
Python以外にも、回帰分析を行えるツールがあります。以下はその一部です。
1. Excel
- 特長: 手軽に回帰分析が可能。小規模データ向け。
- 用途: 線形回帰、多重回帰(分析ツールのアドインを活用)。
- 利点: データ入力と簡単な分析が一体化。
2. R
- 特長: 統計解析に特化した言語。豊富な回帰モデルライブラリ。
- 用途: 線形回帰、非線形回帰、分位点回帰など。
- 利点: 統計指標やモデル評価が詳細。
3. MATLAB
- 特長: 数値計算に強みを持つ。科学技術分野での利用が多い。
- 用途: 線形回帰、多重回帰、曲線フィッティング。
- 利点: 高度なグラフ作成やアルゴリズム実装。
4. Tableau
- 特長: データ可視化ツール。統計モデルをグラフ化。
- 用途: 基本的な回帰分析、トレンド分析。
- 利点: 視覚的にモデルを説明可能。
5. IBM SPSS
- 特長: 統計解析ソフトウェア。回帰分析機能が強力。
- 用途: 線形回帰、多重回帰、ロジスティック回帰。
- 利点: 統計的な精度が高く、レポート作成も簡単。
研究室や企業によって決められているツールがある方も多いと思います。
環境や目的に合ったツールを使用してください。
ビジネスにおける回帰分析の活用事例と実践的な価値
では、回帰分析は実際にビジネスでどのように活用されているでしょうか。
業界別にご紹介します。
| 業界 | 使用事例 | 目的 |
|---|---|---|
| 小売業 | 売上予測、需要予測、商品の価格設定 | 広告費や気温などの要因が売上に与える影響を分析し、需要変動や価格戦略を最適化する。 |
| 製造業 | 生産効率の向上、不良品率の予測、設備保全計画 | 温度、湿度、稼働時間が製品品質や機械の故障率に与える影響を分析し、生産プロセスを改善する。 |
| 金融業 | 株価予測、リスク評価、顧客信用スコアの算出 | 経済指標や顧客属性が株価や信用スコアに及ぼす影響を把握し、リスク管理や投資戦略を構築する。 |
| ヘルスケア | 疾患リスク予測、医療費の推定、患者リハビリの進捗分析 | 遺伝的要因や生活習慣が疾患発症リスクに与える影響を分析し、予防医療やコスト管理に役立てる。 |
| IT・テクノロジー | ユーザー行動予測、アプリ利用率分析、クリック率の最適化 | 時間帯やデバイス使用状況がアプリの利用率や広告クリック率に与える影響をモデル化し、UXを向上。 |
| 交通・物流 | 配送時間の予測、交通量の予測、車両メンテナンス計画 | 天候や曜日が配送時間や交通量に及ぼす影響を分析し、効率的な運行計画や物流管理を行う。 |
| 教育 | 学生の学力予測、進学率の分析、学習支援システムの効果測定 | 学習時間や環境が成績に与える影響をモデル化し、学習指導や教育政策の改善に活用する。 |
| エネルギー | 電力需要予測、設備メンテナンス計画、再生可能エネルギーの発電量予測 | 季節や気象条件がエネルギー需要や発電量に及ぼす影響を把握し、安定供給とコスト削減を実現する。 |
| 農業 | 作物収量予測、病害リスク分析、土壌改良計画 | 気温、降水量、土壌成分が作物の収量や病害発生リスクに与える影響を分析し、生産性を向上させる。 |
| 不動産 | 物件価格予測、地域ごとの需要分析、賃貸収益の最適化 | 立地条件や周辺環境が物件価格や需要に及ぼす影響を把握し、価格設定や投資判断を支援する。 |
これらの事例を参考に、回帰分析の幅広い応用範囲を理解することで、業務効率化や収益向上に役立てることができます。
まとめ
本記事は、機械学習における回帰分析の基礎から応用、そして最新のトレンドまでを網羅的に解説しました。回帰分析は連続値を予測する中心的な手法であり、数値予測、特徴量の影響評価、モデルの解釈性を通じて、ビジネスや科学研究に広く応用されています。
PythonやRといった強力なプログラミングツールを活用することで、回帰モデルの構築と可視化がより柔軟に実現可能です。
回帰分析は非常によく使われる分析手法の一つですのでぜひ本記事が皆様のお役に立てると幸いです。
AI総合研究所では、AIや統計学の応用と研究を通じて、次世代のAIシステムを開発しています。
学術研究と社会実装の橋渡しを行い、よりスマートで持続可能な未来の構築に貢献します。
AI導入のご相談、開発依頼などお気軽にAI総合研究所にご相談ください。