この記事のポイント
特徴量が多すぎてモデル精度が伸び悩む場合、PCAによる次元削減が前処理の第一候補- 顧客分析やマーケティングデータの可視化には、2〜3主成分への圧縮が実務的に最も効果的な手法
- scikit-learnのPCAモジュールなら数行で実装でき、初期検証コストの低さが最大の利点
- 寄与率80%以上を目安に主成分数を決めるのが基本方針であり、過度な圧縮は情報損失のリスクがある点に注意
- 非線形構造が強いデータにはPCAは不向きで、Kernel PCAやt-SNEへの切り替えが次の検討事項
Microsoft AIパートナー、LinkX Japan代表。東京工業大学大学院で技術経営修士取得、研究領域：自然言語処理、金融工学。NHK放送技術研究所でAI、ブロックチェーン研究に従事。学会発表、国際ジャーナル投稿、経営情報学会全国研究発表大会にて優秀賞受賞。シンガポールでのIT、Web3事業の創業と経営を経て、LinkX Japan株式会社を創業。
主成分分析（PCA）とは、多数の変数を持つデータを情報をできるだけ保持しながら少ない軸に圧縮する次元削減技術であり、機械学習の前処理・データ可視化・異常検知など幅広い分野で活用される基本手法です。
本記事では、主成分分析の基本概念と仕組み、Pythonによる実装例、顧客データ・画像データの実例、機械学習・マーケティング・異常検知での活用シーン、注意点まで体系的に解説します。
主成分分析とは？
主成分分析イメージ画像
主成分分析とは、複数の変数があるデータから、本質的な情報をできるだけ保持しながら、次元（軸）の数を減らす技術です。
たとえば「身長」と「体重」という2つの指標を、「体格」という1つの概念でまとめるようなイメージに近いです。
もともと膨大な情報を持つデータを、より少ない指標で表現することで、
- データの可視化が容易になる
- モデルの過学習リスクを減らせる
- 処理速度が向上する
といったメリットが得られます。
なぜ主成分分析が必要なのか？
次元の呪いと主成分分析
現代のデータは、多数の特徴量（変数）を持つことが一般的です。
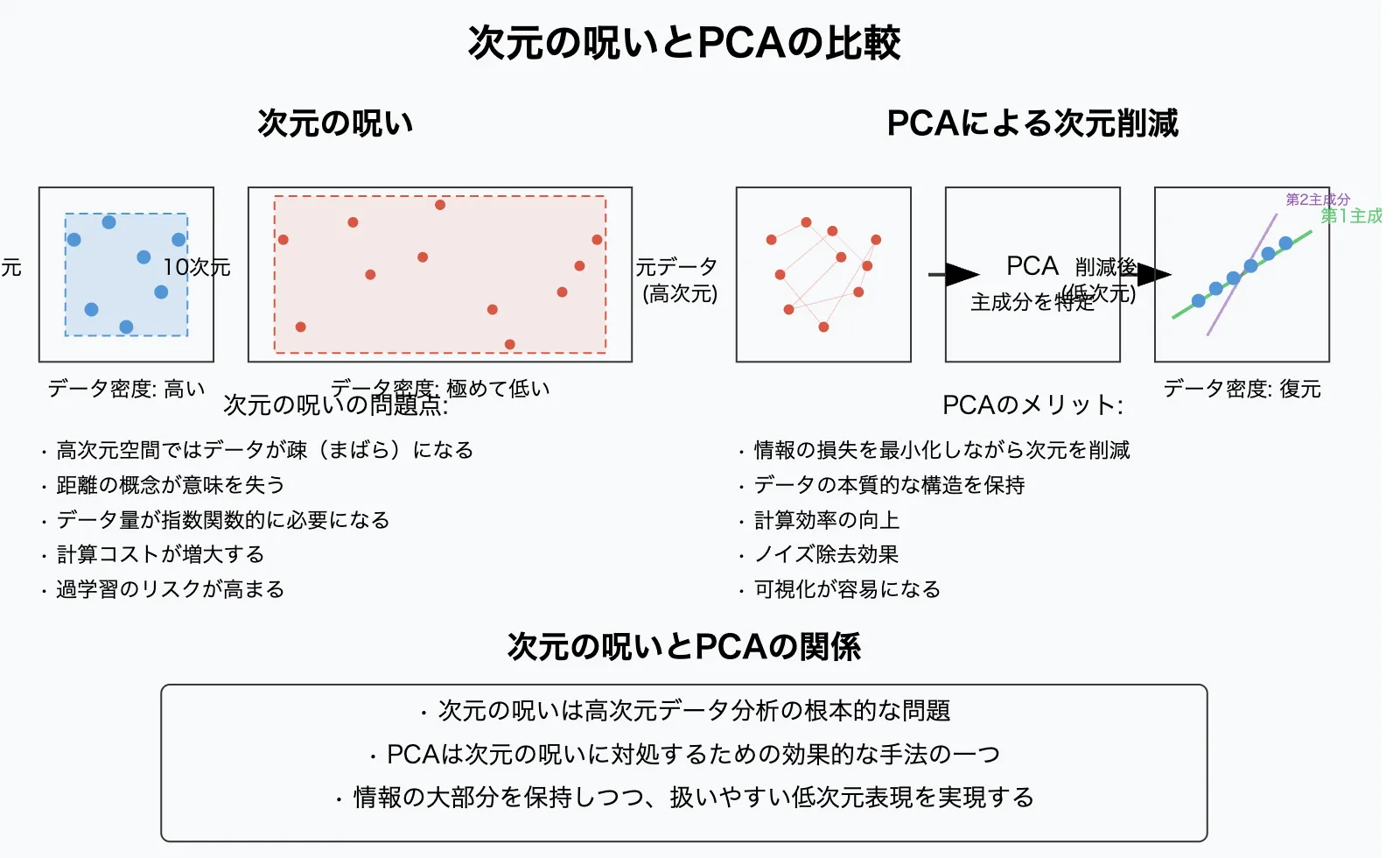
しかし、次元数が増えると、分析や学習が難しくなる**「次元の呪い（Curse of Dimensionality）」**という問題が発生します。
- データが疎になり、統計的に意味のある分析が難しくなる
- モデルの学習が過学習しやすくなる
- データ可視化（グラフ化）が困難になる
こうした問題を解決するために、
「できるだけ情報を保ちつつ、次元を減らす」＝主成分分析が使われるのです。
主成分分析により、
- 重要な情報は残しながら
- 冗長な情報やノイズを排除して
- シンプルで扱いやすいデータに変換できます。
主成分分析の仕組みを簡単に
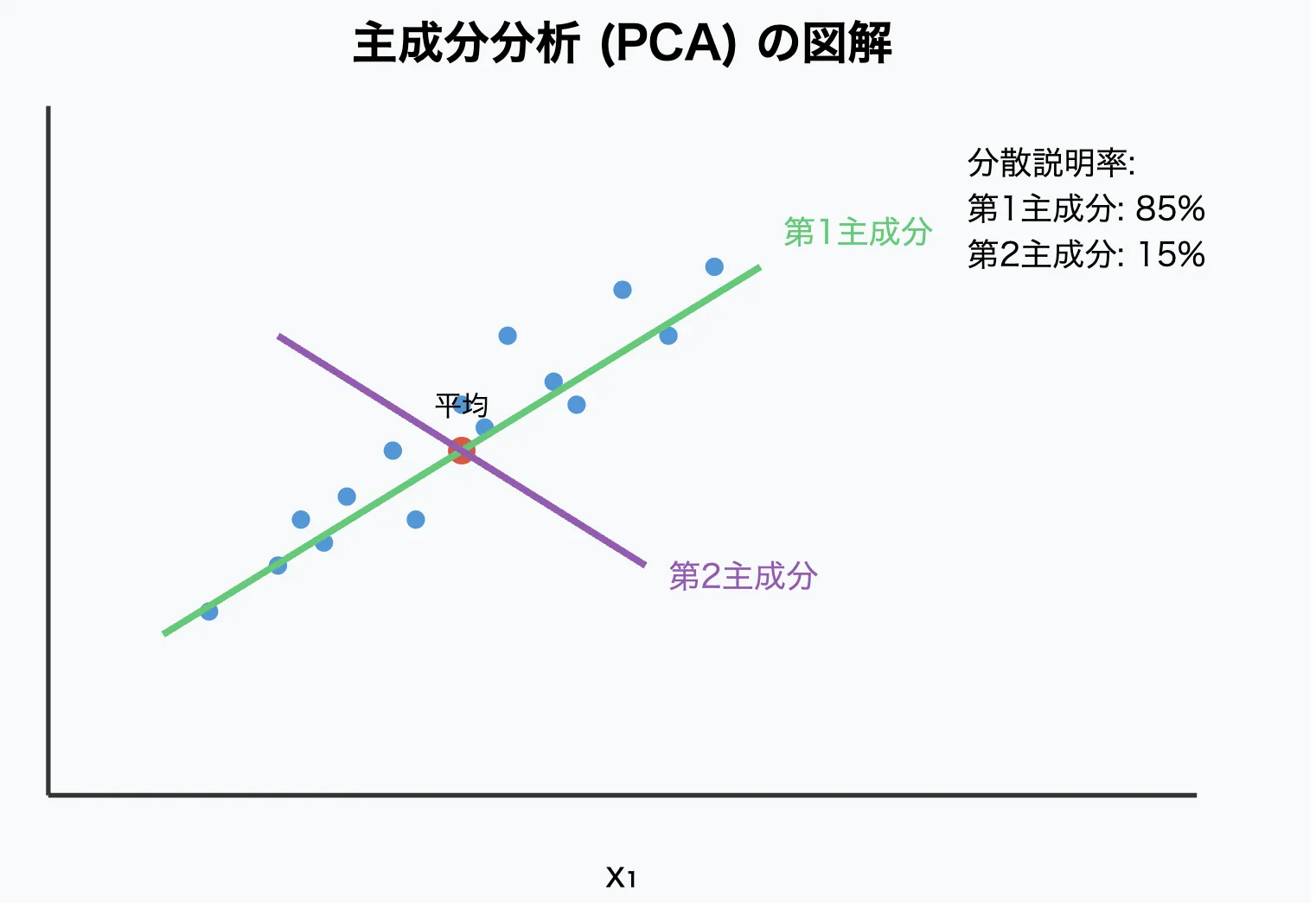
主成分分析のコアアイデアは、「データの分散（ばらつき）が最大になる方向を探す」 ことです。
つまり、データが広がっている方向に新たな軸（主成分）を取ります。
大まかな流れは以下の通りです。
- データを標準化する（スケールを揃える）
- 共分散行列を計算する（各特徴量同士の関連を測る）
- 共分散行列の固有ベクトルと固有値を求める
- 固有値の大きい順に、主成分として採用する
ここで重要なのは、
固有ベクトル＝新しい軸（主成分）
固有値＝その軸がどれだけデータを表現できるかの指標
ということです。
直感的には、
「ばらつきが大きい方向に新しい座標軸を取ることで、できるだけ情報を保持する」
と覚えておけば十分です。PCAの数学的背景と各種次元削減手法の比較はscikit-learn公式の次元削減ガイドで詳しく解説されています。
Pythonで簡単に主成分分析を試してみよう！
実際の実行コード
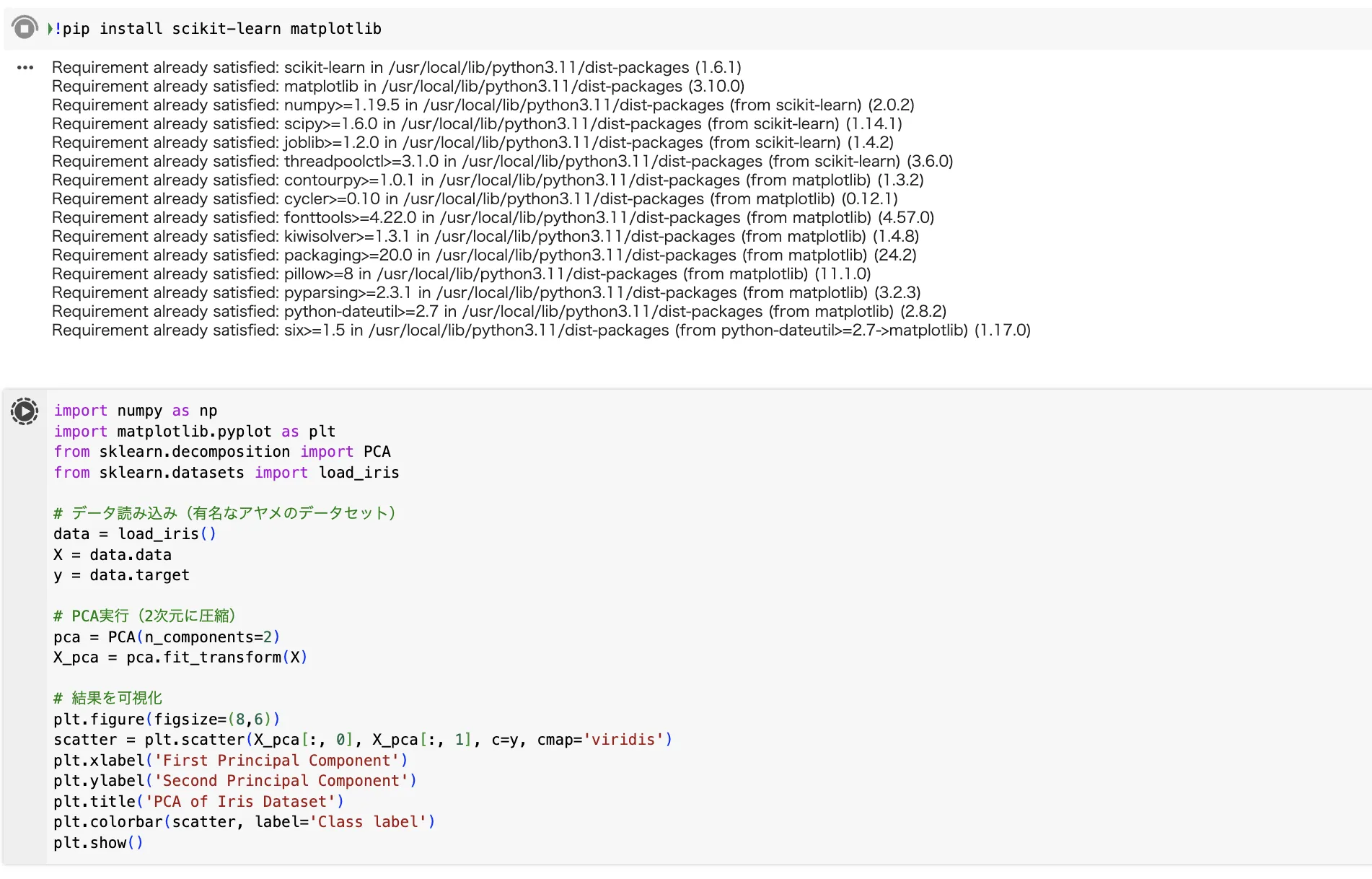
ここでは、Pythonライブラリscikit-learnを使って、簡単な主成分分析（PCA）を実装してみます。PCAの詳細なパラメータはscikit-learn公式のPCA APIリファレンスで確認できます。
必要なライブラリ
!pip install scikit-learn matplotlib
コード例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
# データ読み込み（有名なアヤメのデータセット）
data = load_iris()
X = data.data
y = data.target
# PCA実行（2次元に圧縮）
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 結果を可視化
plt.figure(figsize=(8,6))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA of Iris Dataset')
plt.colorbar(scatter, label='Class label')
plt.show()
実行結果のイメージ
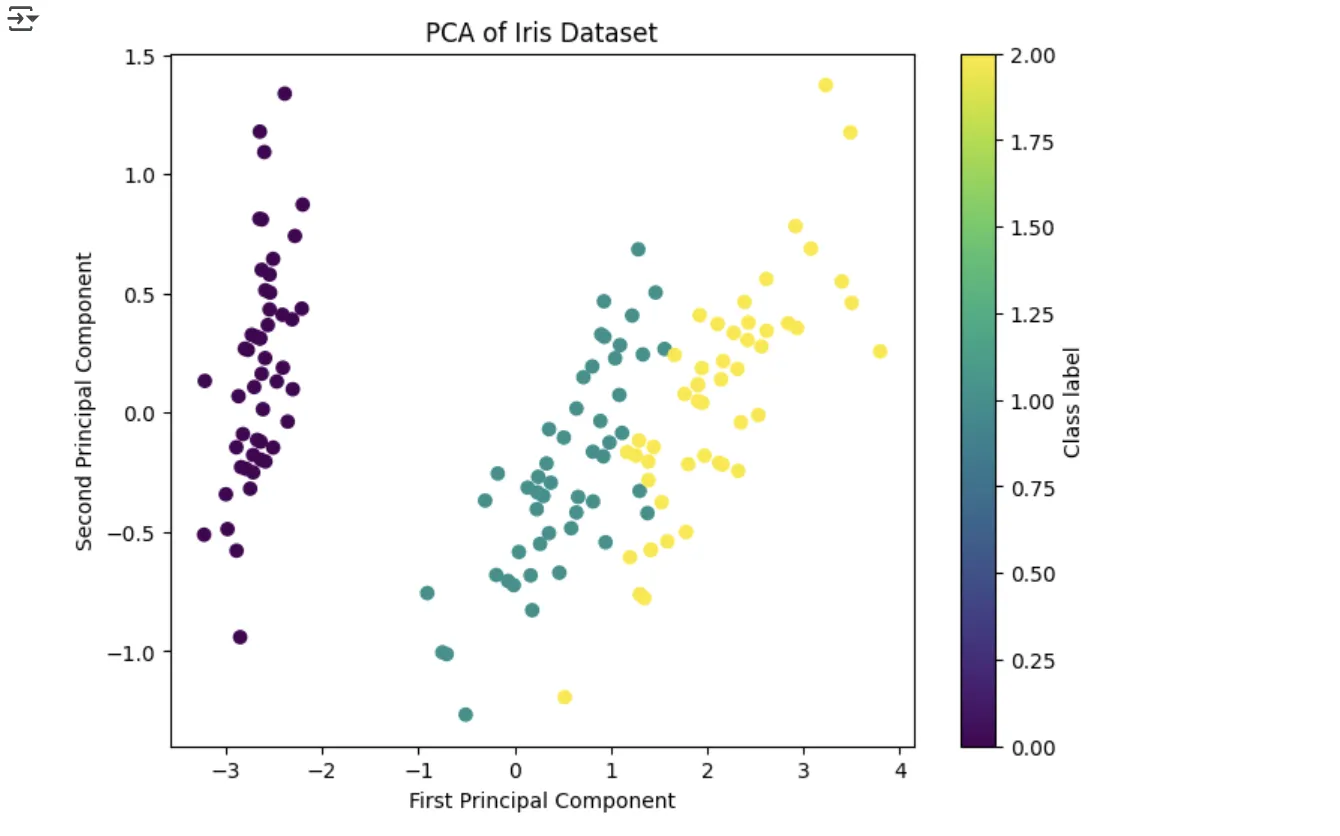
実際の出力結果
- もとの4次元データ（花びらの長さ・幅など）が2次元に圧縮され、分類パターンが可視化される
- 主成分軸に沿って、異なるクラス（花の種類）がある程度きれいに分かれる
主成分分析の実例（簡単なケーススタディ）
主成分分析がどのように役立つのか、具体例を見ていきます。
例①：顧客データの要約
ある企業が、顧客の「年齢」「年収」「購買回数」など多数の変数を持っているとします。
これらを主成分分析でまとめると、たとえば
- 第1主成分：顧客の購買意欲
- 第2主成分：年齢・所得水準
のように、ビジネス的に意味のある軸に要約できます。
例②：画像データの次元削減
顔写真など高次元なデータも、主成分分析によって特徴的な成分だけを抽出し、データサイズを大幅に削減できます。
これにより、認識モデルの学習速度が向上し、精度も改善することがあります。
主成分分析の活用シーン
主成分分析（PCA）は、単なる次元削減にとどまらず、データの本質的な構造を明らかにし、意思決定やアルゴリズム性能に直接貢献する重要な役割を果たしています。
ここでは、特に実務で威力を発揮する具体的な活用シーンを深掘りして紹介します。
| 活用領域 | 主成分分析が果たす役割 |
|---|---|
| 機械学習 | 特徴量圧縮、学習高速化、汎化性能向上 |
| データ可視化 | 構造発見、仮説生成、パターン認識 |
| 異常検知 | 正常・異常の判別容易化 |
| マーケティング | 潜在指標抽出、ターゲティング精度向上 |
| リアルタイム処理 | ストリームデータ圧縮、通信・計算負荷軽減 |
1. 機械学習モデルの前処理：精度と学習効率の最適化
高次元データに対するモデル学習は、次元の呪いによりパフォーマンスが低下しやすくなります。
主成分分析を適用することで、情報を極力保持しながら特徴量を圧縮し、
- 学習スピードの向上
- 過学習リスクの低減
- モデル汎用性の向上
を同時に実現します。
特に、回帰分析、SVM、ニューラルネットワークなど次元に敏感なアルゴリズムとの相性が非常に良いです。
2. 高次元データの可視化：隠れた構造を浮かび上がらせる
PCAを用いることで、もともと人間が認識できない高次元データ（100次元、1000次元規模）を2次元または3次元に落とし込み、
- クラスタリング構造
- 異常点（外れ値）
- データ間の関係性
を直感的に把握できるようになります。
データ探索フェーズでのPCAプロットは、仮説構築や次ステップのモデリング方針決定に極めて有効です。
3. 異常検知：正常分布からの逸脱を捉える
高次元空間では、単純な距離ベースの異常検知が困難になります。
PCAによって、主要なばらつきを捉える低次元空間に射影することで、
- 正常データは主成分空間内に密集
- 異常データは外れた位置に現れる
という分離性が生まれます。
特に製造ライン監視、クレジットカード不正検知、セキュリティ分野での活用が進んでいます。
4. マーケティングデータ分析：多変量特徴の本質的要約
消費者行動データやアンケート調査データは、無数の変数（質問項目、行動ログ）を持ちます。
主成分分析により、
- 顧客関心度
- 購買意欲
- ブランド親和性
といった潜在的な構造を抽出し、少数の指標に要約できます。
この要約結果をもとに、ターゲティング、パーソナライズ、セグメント別施策立案ができるようになります。
5. 次世代データパイプラインへの組み込み：リアルタイム適応処理
近年では、PCAを単なる事後分析だけでなく、
- ストリームデータ処理
- エッジAIデバイス上での次元圧縮
- リアルタイム異常検知
といった即時処理パイプラインにも組み込む事例が増えています。
PCAを事前に適用して情報量を減らすことで、通信負荷や計算負荷を劇的に削減しつつ、即応性を損なわない設計ができます。
主成分分析の注意点
便利な主成分分析にも注意すべきポイントがあります。
-
情報の一部損失
主成分数を減らすことで、どうしても細かな情報は失われる -
主成分の意味づけが難しい
抽出された主成分が、必ずしもビジネスで直感的にわかりやすいとは限らない -
標準化の必要性
単位やスケールが違うデータ（例：身長と収入）をそのまま扱うと、正しい主成分が得られないため、事前に標準化が必要なケースが多い。PCAを適用する際のスケーリングと前処理についてはscikit-learn公式の前処理ガイドで確認できます
データ分析手法の知識を業務へのAI導入に結びつける
主成分分析の理解から業務データのAI活用へ
主成分分析のような統計手法を理解した方なら、AIがデータをどう処理するかの基礎が身についています。220ページの実践ガイドで、データ分析の知識を業務プロセスのAI化に活かす方法を確認できます。
データ分析の知識を業務へのAI導入に結びつけるなら
主成分分析のような統計手法を学んだことで、データの構造を見抜く力が身についたはずです。この知識は、AIが業務データをどのように処理し、意味のあるアウトプットを生み出すかを理解する上でも大きな強みになります。
AI総合研究所では、データ分析の基礎知識を持つ方が業務プロセス全体をAIで効率化するための実践ガイドを公開しています。220ページの資料で、統計分析からAI導入まで段階的に進める手順をまとめています。
データ分析の知見を活かして、自社の業務にAIを導入する計画を立ててみてください。
データ分析手法の知識を業務へのAI導入に結びつける
主成分分析の理解から業務データのAI活用へ
主成分分析のような統計手法を理解した方なら、AIがデータをどう処理するかの基礎が身についています。220ページの実践ガイドで、データ分析の知識を業務プロセスのAI化に活かす方法を確認できます。
まとめ
本記事では、主成分分析（PCA）の基本概念から仕組み、Pythonでの実装、実例、活用シーンと注意点まで体系的に解説しました。
この記事で得られる3つの価値は以下の通りです。
-
次元削減の基本技術としてのPCA
主成分分析は、複数の変数を持つデータから情報をできるだけ保持しながら次元を削減する技術であり、データの可視化・過学習防止・処理速度向上に直結します。固有ベクトルが新しい軸、固有値がその軸の情報量を表すという基本原理を理解しておけば、実務での応用判断に役立ちます。 -
scikit-learnによる即実践の実装力
scikit-learnのPCAモジュールを使えば数行のPythonコードで主成分分析を実行でき、Irisデータセットのような4次元データを2次元に圧縮して可視化できます。寄与率80%以上を目安に主成分数を決めるのが基本方針です。 -
多分野での活用と適用限界の理解
機械学習の前処理、高次元データの可視化、異常検知、マーケティング分析、リアルタイムデータパイプラインなど、PCAの適用領域は広範です。一方、非線形構造が強いデータにはPCAは不向きなため、Kernel PCAやt-SNEへの切り替えを検討してください。
PCAの導入を検討する場合は、まずscikit-learnのPCAモジュールで手持ちのデータを2〜3次元に圧縮し、散布図で構造を確認するところから始めてください。
