この記事のポイント
この記事はサポートベクターマシン(SVM)について詳しく解説しています。
非線形や高次元データに適用可能な機械学習手法であり、ハイパープレーンを用いた明確な決定境界を持つことが特長です。

Microsoft MVP・AIパートナー。LinkX Japan株式会社 代表取締役。東京工業大学大学院にて自然言語処理・金融工学を研究。NHK放送技術研究所でAI・ブロックチェーンの研究開発に従事し、国際学会・ジャーナルでの発表多数。経営情報学会 優秀賞受賞。シンガポールでWeb3企業を創業後、現在は企業向けAI導入・DX推進を支援。
データ分析や予測モデルを構築するにあたり、適切な機械学習手法の選択が欠かせません。多くの手法が存在する中で、特に注目されているのがサポートベクターマシン(SVM)です。非線形データや高次元データに強く、少ないサンプルからも高い予測精度を得ることができるため、幅広い分野において有効な手法として利用されています。この記事では、SVMの基本的な概念から、その動作原理、カーネル手法の利用、さらに実際の応用事例に至るまで、SVMの全貌について、初心者にもわかりやすく解説していきます。また、他の機械学習手法との比較や、実践に役立つ具体的なアプローチ方法も紹介します。SVMの強みを活かしたデータ解析の基礎を学んで、実際の問題解決にこの手法を適用してみましょう。
目次
1. C-SVC(C-Support Vector Classification)
2. ν-SVC(ν-Support Vector Classification)
3. SVR(Support Vector Regression)
3. スパムメールフィルタリング(SpamAssassin)
サポートベクターマシン(SVM)とは
サポートベクターマシン(Support Vector Machine、SVM)は、機械学習の分野で広く用いられる分類および回帰手法の一つです。
SVMは、データを特徴空間上で分離する「境界線(ハイパープレーン)」を求めることで、ラベルを予測します。
特徴は、分離マージンを最大化することで決定境界の汎化性能を高める点にあり、高次元かつ複雑なデータでも適用可能であることから、各種タスクで有効な手段として知られています。
SVMの基本的な考え方
本記事ではSVMの詳細を解説していきますが基本的な考え方をしっかりとイメージしておいてください。
押さえておきたいポイントは2つです。
-
データの分け方
データがどちらのグループに属するかをはっきり分けるため、ハイパープレーンを使います。
このハイパープレーンは、「できるだけ広い余裕(マージン)」を持つように調整されます。これにより、新しいデータにも対応しやすくなります。 -
重要なデータ点
ハイパープレーンに一番近いデータ点を 「サポートベクター」 と呼びます。このサポートベクターが、ハイパープレーンの位置を決める鍵になります。
なぜSVMが注目されるのか
その理由は大きく3つです。
-
高次元データにも強い
特徴(データの要素)が多い場合でも、SVMは良い性能を発揮します。 -
非線形の問題も解ける
データが単純に線で分けられない場合でも、特殊な関数(カーネル関数)を使って、複雑なデータの分類が可能です。 -
精度が高い
分離マージンを最大化する仕組みにより、新しいデータに対する予測が安定します。
以上のことから、SVMは、データが高次元であっても比較的安定した性能を示し、適切なカーネル関数を選べば非線形問題にも対応できます。また、ハイパープレーンを用いた明確な決定境界は、ロジスティック回帰などの線形モデルよりも柔軟な表現力を持ち、説明可能性と高精度を両立する手法として注目を集めてきました。

SVMでのりんごとオレンジの分類イメージ
非線形の問題も解ける、線形分離とは
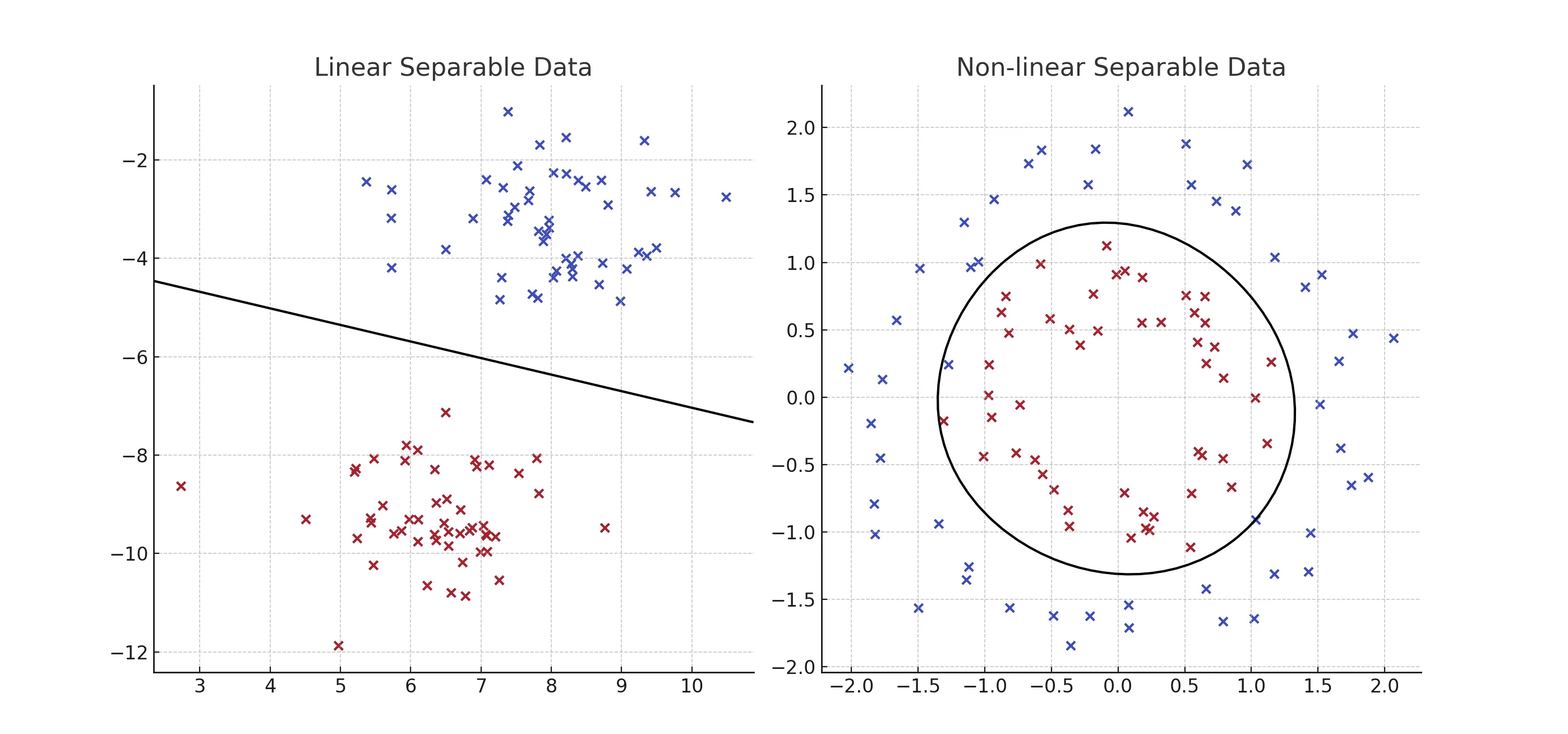
左:線形分離、右:非線形分離のイメージ図
- 線形分離:
赤い点と青い点がきれいに分かれている。1本の直線で分けられる。 - 非線形分離:
赤い点がリング状に分布し、その中に青い点がある。直線では無理なので、次元を増やして分離する。
線形分離とは、データ点が直線(または平面、次元が高ければハイパープレーン)によって完全に分けられる状態を指します。たとえば、2次元平面で考えると以下のようなイメージです:
- 赤い点と青い点がそれぞれ異なるクラスに属している。
- 一本の直線を引けば、赤い点と青い点を完全に分けることができる。
例えば、ハイパープレーンが赤い点と青い点の間にぴったり配置されていて、どちらにも近すぎない場合、それが「最適な線形分離」となります。
数式的に表すと:
- ( w ) はハイパープレーンの「向き」を決めるベクトル(直線の傾きみたいなもの)。
- ( b ) はハイパープレーンの「位置」を調整するための定数。
ハイパープレーン上の点は以下の式で表されます:
[
w \cdot x + b = 0
]
すべてのデータ点が以下を満たす必要があります:
[
y_i (w \cdot x_i + b) \geq 1
]
ここで:
- ( y_i ) はその点のクラス(+1または-1)。
- ( x_i ) はその点の座標。
非線形分離とカーネル法
現実のデータでは、必ずしも直線や平面で分けられるとは限りません。以下のようなケースを考えてみましょう。
- 赤い点と青い点がリング状に配置されていて、直線では分けられない。
このような場合、非線形分離が必要です。SVMはこれを「カーネル法」という手法で解決します。カーネル法のイメージを以下のように説明できます:
-
次元を増やす
例えば、2次元のデータ(平面上)を3次元空間に「持ち上げる」ことで、データをより分離しやすくします。- 2次元では丸いデータ分布(円形)でも、3次元に持ち上げれば、平面で分けられるようになります。
-
カーネル関数を使う
直接次元を増やさず、カーネル関数を使って「データ間の関係性(類似度)」を計算し、高次元空間での分離を効率的に実現します。
よく使われるカーネル関数には以下があります:- 線形カーネル:実質的に線形分離と同じ。
- 多項式カーネル:データを曲線的に分離。
- RBF(ガウシアン)カーネル:非線形データに対して非常に強力。
カーネル法のおかげで、実際には次元を増やす計算をしなくても、非線形なデータを線形的に扱えるようになります。
SVMの種類とその拡張方法ついて
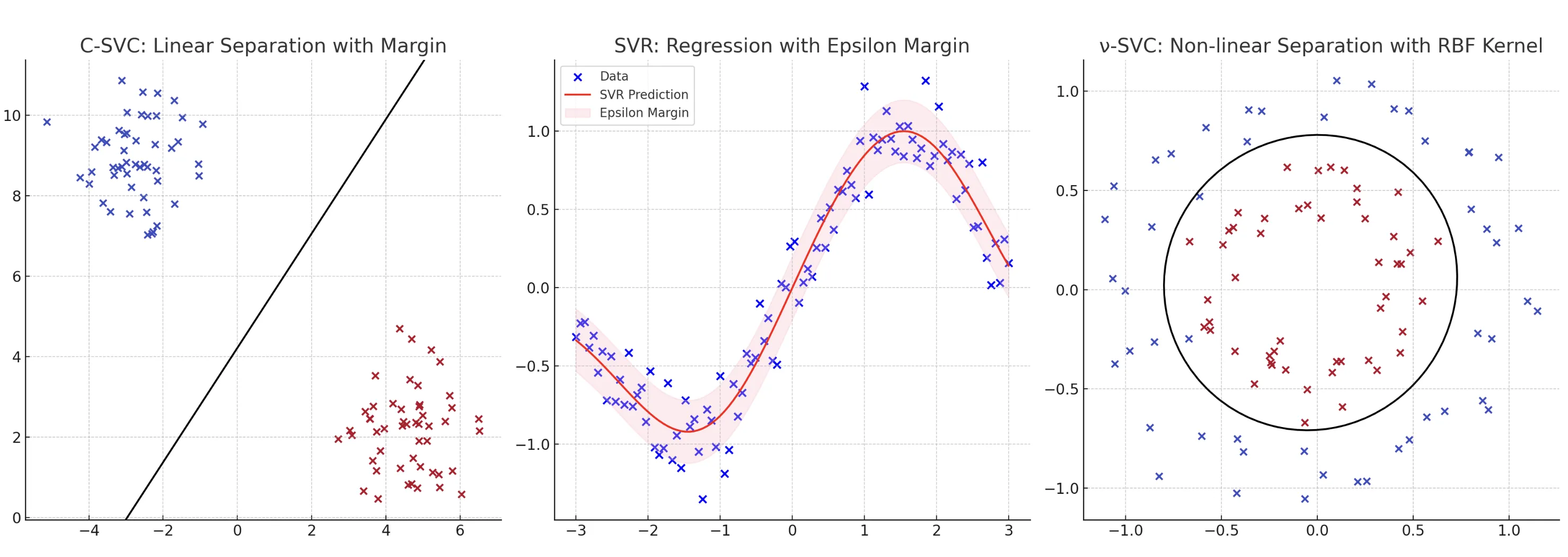
左からC-SVC、ν-SVC、SVR
以下は、SVMの種類とその拡張について、わかりやすく説明します。
1. C-SVC(C-Support Vector Classification)
- C-SVCは「標準的なSVM」で、多少の誤分類を許容しながら、分離マージン(データ間の余裕)を最大化することを目的とします。
- パラメータ ( C ) は、以下のトレードオフを調整します:
- 大きなマージン:誤分類を許容しやすい(柔軟な境界)。
- 少ない誤分類:マージンが小さくなり、境界がデータに厳密にフィット。
例:
( C ) を小さくすると、境界が滑らかになり、多少の誤分類を許容する。
( C ) を大きくすると、境界がデータに厳密にフィットし、誤分類を減らす。
2. ν-SVC(ν-Support Vector Classification)
- C-SVCと似ていますが、代わりにパラメータ (\nu) を導入しています。
- (\nu) は次のような特性を持つトレードオフを調整します:
- マージンの広さ。
- サポートベクター(境界に近いデータ点)の数。
3. SVR(Support Vector Regression)
- 回帰問題(連続値を予測する問題)にSVMを適用する形式です。
- 予測モデルが「ハイパーチューブ」という範囲内にデータを収めるように学習します。このチューブは「誤差範囲」とみなされます。
動きの仕組み:
- データがこのハイパーチューブ内に収まっていれば「正解」とみなします。
- チューブ外のデータにはペナルティを課して調整します。
例:
- 価格予測や気温予測など、数値データの回帰に使用されます。
4. 多クラス分類
SVMは本来、2クラス(Aクラス vs Bクラス)の分類を行う手法ですが、複数のクラスを分類するために次の拡張方法が利用されます。
One-vs-Rest法
- 各クラスと「それ以外のすべてのクラス」を比較するモデルを構築します。
- クラス数が (N) の場合、(N) 個の分類モデルを作ります。
- 例: 犬 vs (猫と鳥)、猫 vs (犬と鳥)、鳥 vs (犬と猫)
One-vs-One法
- すべてのクラスのペアについてモデルを作成します。
- クラス数が (N) の場合、(\frac{N(N-1)}{2}) 個の分類モデルを作ります。
- 例: 犬 vs 猫、犬 vs 鳥、猫 vs 鳥
選び方としては、データが少ない場合は One-vs-Rest 法が効率的でデータが多く、計算リソースが豊富な場合は One-vs-One 法が高い精度を出しやすい手法となります。
これらの違いを考えることで、SVMの手法を選択しやすくなります。
実践的なアプローチ方法の紹介
-
基本設定から開始:
RBFカーネルを用い、(\gamma = 1 / \text{特徴数})、(C = 1) などの一般的な初期値で学習を開始します。 -
パラメータ範囲を絞る:
初期モデルの性能を基に、(\gamma) や (C) の範囲を狭め、再調整を行います。 -
複数の評価指標を使用:
精度、F1スコア、AUC-ROCなど、タスクに適した指標で最適なパラメータを選択します。
SVMの性能を最大限に引き出すには、カーネル選択、ペナルティパラメータ (C)、カーネルパラメータ (\gamma) などの調整が重要です。グリッドサーチやベイズ最適化を利用しながら、クロスバリデーションでモデルの汎化性能を検証することで、最適な設定を見つけることができます。
実際に実装してみましょう
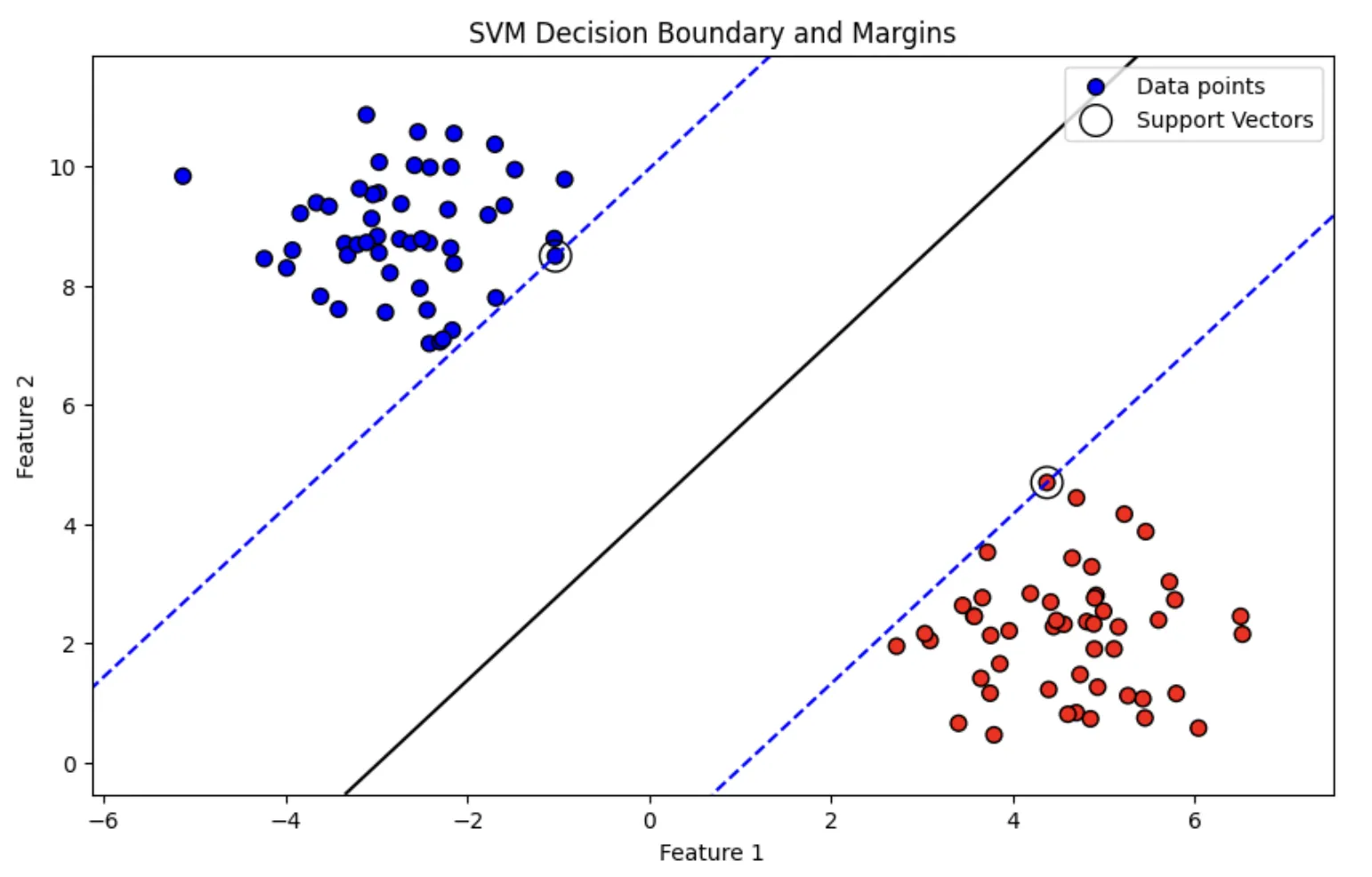
実行結果のSVM画像
以下は、Google ColabでSVMを実装するためのサンプルコードです。このコードでは、2次元データを用いて、SVMがどのようにデータを分類するかを視覚的に理解できることを目的とします。
# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_blobs
# データセットの作成
X, y = make_blobs(n_samples=100, centers=2, cluster_std=1.0, random_state=42)
y = 2 * y - 1 # ラベルを -1, 1 に変更(SVMの基本設定に合わせる)
# SVMモデルの作成と学習
model = SVC(kernel='linear', C=1)
model.fit(X, y)
# ハイパープレーンとマージンの描画関数
def plot_svm_decision_boundary(model, X, y):
# サポートベクターの取得
support_vectors = model.support_vectors_
# グラフの範囲を設定
xlim = [X[:, 0].min() - 1, X[:, 0].max() + 1]
ylim = [X[:, 1].min() - 1, X[:, 1].max() + 1]
# グリッドを作成
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 200),
np.linspace(ylim[0], ylim[1], 200))
Z = model.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット開始
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.bwr, s=50, edgecolors='k', label='Data points')
# 決定境界(ハイパープレーン)の描画
plt.contour(xx, yy, Z, levels=[-1, 0, 1], colors=['blue', 'black', 'blue'], linestyles=['--', '-', '--'])
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], s=200, facecolors='none', edgecolors='k', label='Support Vectors')
# 範囲の設定
plt.xlim(xlim)
plt.ylim(ylim)
plt.title("SVM Decision Boundary and Margins")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.show()
# ハイパープレーンとマージンを描画
plot_svm_decision_boundary(model, X, y)
実行結果の解釈
黒い実線: ハイパープレーン(データを分離する最適な境界線)。
青い破線: マージン(ハイパープレーンとサポートベクターの距離)。
サポートベクター: 決定境界の位置を決定する重要なデータ点。
このコードをGoogle Colabなどで実行すれば、SVMの動作を直感的に理解できます。ぜひ試してみてください!
他の機械学習手法との比較
サポートベクターマシン(SVM)は、その独自の特性と強みを持ちながらも、他の機械学習手法と使い分ける必要があります。以下では、SVMと代表的な手法との違いを整理します。
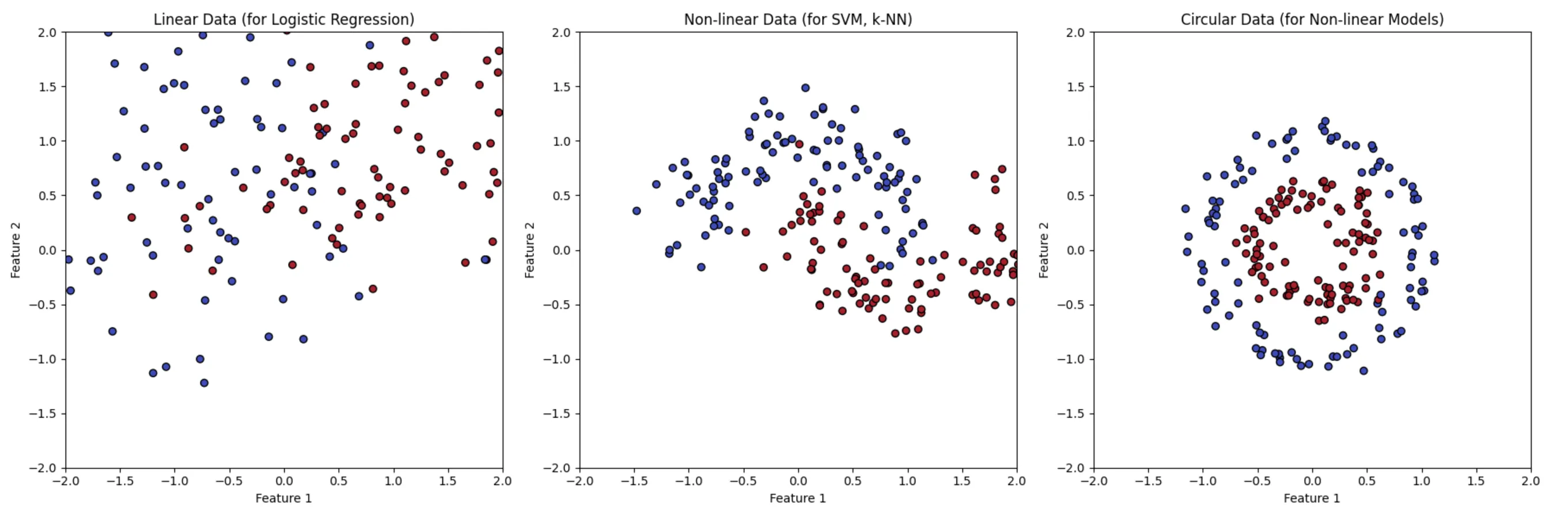
機械学習手法のイメージ
以下は、SVMを他の機械学習手法と比較した表です。
| 手法 | 特徴 | 利点 | 欠点 | 適用場面 |
|---|---|---|---|---|
| SVM | 境界マージンを最大化し、カーネルで非線形分類にも対応 | 少量データ、高次元データに強い。カーネルで柔軟な適応が可能。 | ハイパーパラメータ調整が必要。大規模データでは計算コストが高い。 | 高次元データや少量データ、明確な境界が求められる分類問題(例: 医療診断、テキスト分類) |
| ロジスティック回帰 | 線形モデル。分類境界は直線または平面 | シンプルで高速。結果が解釈しやすい。 | 非線形データには弱い(特徴量変換が必要)。 | 線形分離可能なデータ(例: クリック予測、マーケティング分析) |
| 決定木 | データを分割するルールを階層的に構築 | 解釈性が高い(ツリー構造)。スケール調整が不要。 | 過学習しやすい(特に深い木)。 | 解釈性が重要なタスク(例: 業務プロセス分析、顧客分類) |
| ランダムフォレスト | 複数の決定木をアンサンブルして性能を向上 | 過学習に強い。特徴量重要度が確認できる。 | モデルが複雑で、学習・予測時間が長くなる。 | 非線形データや特徴量間の相互作用が重要な問題(例: 医療診断、気象予測) |
| XGBoost | 勾配ブースティングを活用したアンサンブル学習 | 高い性能。ハイパーパラメータ調整で柔軟性が高い。 | 適切なパラメータ設定に時間がかかる。 | 精度重視のタスク(例: コンペティション、金融リスク評価) |
| k-NN | 最近傍のデータポイントを基に分類 | シンプルで実装が容易。 | 高次元データでは計算コストが高い。ノイズに弱い。 | 少量データ、非線形分類(例: 小規模データの分類タスク、簡易な画像分類) |
| ディープラーニング | ニューラルネットワークを用いて複雑な非線形パターンを学習 | 大量データで非常に高い精度を達成。特徴量設計が不要。 | 訓練に大量の計算資源が必要。過学習リスクが高い。 | 大量データ、画像認識、音声認識、自然言語処理(例: 自動運転、画像分類) |
| ベイズ推定 | 確率モデルに基づき、不確実性を考慮して分類または回帰 | 少量データでも汎化性能が高い。不確実性の定量化が可能。 | 高次元データでは計算が困難。 | 不確実性のモデリングが重要なタスク(例: 医療診断、リスク分析) |
具体的な解説は以下のとおりです。
1. 線形モデルとの比較
-
線形モデル(ロジスティック回帰など)の特徴
- シンプルで解釈性が高い(係数の大きさや符号で影響度が直感的にわかる)。
- 計算が高速で、大規模データに向いている。
- 非線形データには対応が難しい(特徴量変換や多項式回帰が必要)。
-
SVMの強み
- カーネル関数を利用して非線形問題にも対応可能。
- マージン最大化により、新規データへの汎化性能が高い。
-
使い分け
- 線形モデル: 特徴空間が低次元で線形分離が十分な場合。
- SVM: 非線形性が強い問題や、高次元の特徴空間を扱う場合。
【関連記事】
➡️機械学習の回帰の仕組みや実装方法、活用事例を解説
2. 決定木・アンサンブル手法との比較
-
決定木・アンサンブル(ランダムフォレスト、XGBoostなど)の特徴
- 汎用性が高く、特徴量のスケール調整が不要。
- 特徴量の重要度を可視化できるため、解釈性に優れる。
- アンサンブル手法は、過学習に強く、通常のSVMを上回る精度を発揮する場合が多い。
-
SVMの強み
- 適切なカーネルとハイパーパラメータ調整により、少量データでも高精度を実現可能。
- ノイズ耐性が高い(マージン最大化の特性)。
-
使い分け
- 決定木・アンサンブル: データ量が多く、モデル解釈や特徴量の影響分析が重要な場合。
- SVM: 少量かつ高次元のデータや、明確な境界が必要な分類問題。
【関連記事】
➡️ランダムフォレストとは?その仕組みや実装方法、活用事例を解説
3. ディープラーニングとの比較
-
ディープラーニングの特徴
- 大量データと計算資源を活用することで、非常に複雑な非線形パターンを学習可能。
- 画像認識、音声認識、自然言語処理など、データの特徴量設計が困難なタスクで強力。
- 学習には時間と計算コストがかかり、過学習リスクも高い。
-
SVMの強み
- データが少量で特徴量が明確な場合でも、高精度を達成できる。
- モデルのトレーニングが比較的速く、実装がシンプル。
- 適切なカーネル選択で、非線形問題においても高い性能を発揮。
-
使い分け
- ディープラーニング: 大規模データセット、または特徴量抽出が困難なタスク(例: 画像、音声、自然言語)。
- SVM: データ量が少なく、特徴量が明確に設計できる場合(例: 医療データやテキスト分類)。
【関連記事】
➡️ディープラーニングとは?その仕組みや種類、機械学習との違いを解説
4. k近傍法(k-NN)との比較
-
k-NNの特徴
- 非線形データにも柔軟に対応可能で、直感的なアルゴリズム。
- 訓練時間がほとんどかからないが、予測時の計算コストが高い。
- ノイズに弱く、高次元データでは性能が低下しやすい。
-
SVMの強み
- 高次元データでもノイズ耐性が高く、計算効率が良い。
- モデルがトレーニング後に固定されるため、予測が高速。
-
使い分け
- k-NN: 少量データで計算コストを重視しない場合。
- SVM: 高次元データでより明確な分類境界が求められる場合。
5. ベイズ推定との比較
-
ベイズ推定の特徴
- 確率モデルに基づき、不確実性を考慮した予測が可能。
- 少量データで特に強力だが、特徴量数が増えると計算コストが高くなる。
-
SVMの強み
- 高次元データでも計算が可能であり、ノイズに対して堅牢。
- 決定的な分類結果が求められるタスクに適している。
-
使い分け
- ベイズ推定: 不確実性のモデリングが必要な場合(例: 医療診断)。
- SVM: 確率ではなく、明確な分類結果が必要な場合。
【関連記事】
➡️ベイズ統計とは?その仕組みやメリット、活用事例をわかりやすく解説
他の手法と比較しながら、データの特性やタスクの要件に応じてSVMを選択することが重要です。
SVMの活用事例
以下は、SVMが実際に使われた具体的な事例を紹介します。
1. 手書き数字認識(MNISTデータセット)

実際の実行結果イメージ
-
概要:
MNISTデータセットは、0~9の手書き数字画像(28×28ピクセル)で構成される機械学習分野の標準データセットです。 -
SVMの使用:
SVMは、高次元空間における優れた分類性能により、手書き数字認識タスクで高精度を達成しています。特に、RBFカーネルを使用したSVMモデルは、正確な分類性能を示します。 -
成果:
初期のSVMモデルは、MNISTで98%以上の精度を達成し、ニューラルネットワークが一般化する以前の画像分類タスクで重要な成果を挙げました。
2. がん診断(乳がんの分類)
-
概要:
ウィスコンシン乳がんデータセット(Wisconsin Breast Cancer Dataset)は、乳がんの腫瘍が良性か悪性かを判別するために使用されるデータセットです。 -
SVMの使用:
SVMは、腫瘍の特徴(サイズ、形状、質感など)を基に良性・悪性を分類するタスクで使用されています。 -
成果:
SVMは、このデータセットで90%以上の分類精度を達成。特に、限られたデータセットで高い汎化性能を示すことから、医療診断の自動化分野での応用が進んでいます。
3. スパムメールフィルタリング(SpamAssassin)
-
概要:
SpamAssassinは、スパムメールを検出するためのオープンソースフィルタリングシステムで、SVMがそのアルゴリズムに組み込まれています。 -
SVMの使用:
メールの内容やメタデータ(例: 件名、送信者、本文中の単語出現頻度)を特徴量として抽出し、スパムか非スパムかを分類。 -
成果:
SVMは、スパム検出タスクで非常に高い精度を実現し、商用製品やカスタムメールフィルタリングシステムに影響を与えました。
4. 画像認識(顔検出:Viola-Jonesアルゴリズム + SVM)
-
概要:
Viola-Jones顔検出アルゴリズムは、画像から顔領域を検出する高速な方法として知られています。ここにSVMが分類器として統合されています。 -
SVMの使用:
検出された領域が「顔か否か」を判別するためにSVMが利用されています。HOG(Histogram of Oriented Gradients)特徴量と組み合わせて適用。 -
成果:
SVMを用いた顔検出システムは、Webカメラやスマートフォンの顔認証システムに応用されています。
5. 金融詐欺検出(クレジットカード不正利用)
-
概要:
クレジットカード取引データの異常検出にSVMが利用されています。不正利用は通常の取引に比べて非常に少ないため、分類が難しいタスクです。 -
SVMの使用:
不正取引を「異常検知問題」としてモデル化し、SVMを用いて通常の取引との違いを学習。 -
成果:
SVMは、少数派クラス(不正取引)を正確に分類する点で優れており、多くの金融機関で実運用されています。
6. バイオインフォマティクス(遺伝子分類)
-
概要:
遺伝子データから疾患のリスクを特定するためにSVMが活用されています。例えば、DNAマイクロアレイデータを用いた分類。 -
SVMの使用:
高次元で少数のサンプル(遺伝子の発現データ)の特徴を捉えるために、RBFカーネルを使用したSVMが有効。 -
成果:
遺伝子発現パターンから疾患を特定する研究で高精度を達成。がん治療の個別化医療に寄与しています。
7. 音声認識(音素分類)
-
概要:
音声認識システムにおける音素(音の最小単位)の分類にSVMが用いられています。 -
SVMの使用:
MFCC(メル周波数ケプストラム係数)などの音声特徴量を用い、各音素を分類。 -
成果:
初期の音声認識システム(例: Google VoiceやSiriの初期バージョン)で、SVMが採用されていました。
これらの事例は、SVMが幅広い分野で活用されていることを示しています。特に、高次元データや非線形分類が必要なタスクで、その性能が際立ちます。
よくある質問(FAQ)
SVMを使うべきケースは?
データが比較的少なく、明示的な特徴量設計が可能な場合や、非線形な境界が必要な問題でSVMは有効な選択肢となります。
ハイパーパラメータチューニングは必須?
最適なカーネルやC、γなどを試行しなければ、性能が発揮できない場合が多いです。グリッドサーチやクロスバリデーションで調整が一般的です。
大規模データでもSVMは使える?
SVMは計算量的に大規模データに不向きな面がありますが、近似解法や分割学習、オンライン学習手法を用いて拡張することが可能です。
まとめ
本記事では、サポートベクターマシン(SVM)の基本概念や原理(ハイパープレーンとマージン最大化、カーネル手法)、分類・回帰への応用、ハイパーパラメータ調整、代表的な応用事例、他手法との比較、FAQまで包括的に解説しました。
SVMは豊富な理論的背景と汎用性を持ち、依然として多くの応用領域で利用可能な有力な機械学習手法です。適切な特徴量設計やハイパーパラメータ調整を行うことで、強力なモデルを構築できる点から、研究・ビジネス問わず幅広く採用されています。
AI総合研究所では、強化学習の理論と応用の研究を通じて、次世代のAIシステムを開発しています。
学術研究と社会実装の橋渡しを行い、よりスマートで持続可能な未来の構築に貢献します。
AI導入のご相談、開発依頼などお気軽にAI総合研究所にご相談ください。